
多治見市モザイクタイルミュージアム
今日は、岐阜県多治見市にやってきました。ますりん、あそこに不思議な建物があるね。
うふふふ、みさきさん、あれが「多治見市モザイクタイルミュージアム」だよ。釉薬を使った磁器のモザイクタイルは、ここ多治見市笠原町が発祥の地。生産量も全国一なんだ。
あっ。タイルといえば、前に行った博物館を思い出すね。
「モザイク」という言葉は、あっちでも出てきたよ。ええと、確かメソポタミアのモザイク模様が……なんだったっけ?
よく覚えているなぁ。さすが、タイルが大好きな、しほさんだ。愛知県常滑市の「世界のタイル博物館」には、紀元前3500年頃のメソポタミアのタイル模様が再現されていたね。その方法がローマに伝わって、ギリシア神話に出てくる芸術と学問の女神「Mosai(ムーサイ)」に捧げられた洞窟に使われたことから、「mosaic(モザイク)」という言葉ができたんだ。実は「ミュージアム(博物館・美術館)」も、「ミュージック(音楽)」も、このムーサイが語源なんだよ。
わぁ、今までに見たものが、どんどんつながっていく。ドキドキするな。早く中を見にいこうよ……。えっ、これもモザイクタイル? 模様というより、これはもう、絵だね。すごく細かいけど、よく見ると正方形の「しきつめ」になってる。

みさきさん、その通りだね! 同じ正方形のタイルを、色を変えてしきつめることで、絵を作っているんだ。
この柱は、もっと模様っぽいよ。長方形のタイルだね。正方形も長方形もひとつの角の大きさが全部90°で、4つ合わせると360°になる。だから、ぴったりしきつめられるんだ。

正三角形ならひとつの角の大きさは60°だから6つ合わせればいいし、正六角形なら120°だから、3つ合わせればいい。でも、たとえば正五角形だと、どうなるかな? ひとつの角の大きさは108°だから、3つ合わせると324°で、ぴったり360°にならないんだよね……。
しほさん、こっちも見てみて。いろいろなパターンがある。

すごい! いろいろな並べ方があるなぁ。あっ。これ、五角形と正方形を組み合わせてるんじゃない?

本当だ。ええと、まず同じ形の五角形を4つ合わせて、正八角形にしたのかな。でも正八角形だけだとしきつめられないから、すきまに正方形を入れちゃった?
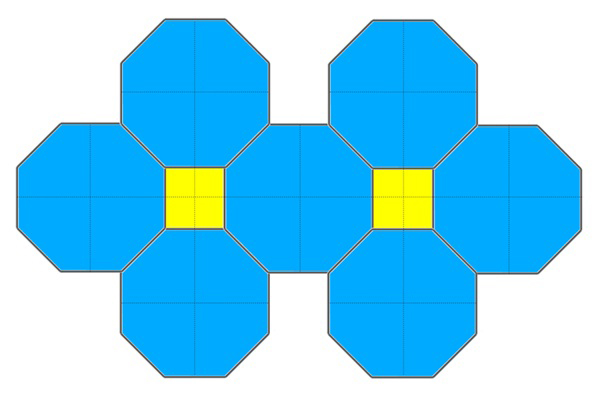
あははは、きっと、そうやって考えたんだね。正多角形を、2種類組み合わせる方法だ。でも、もっと複雑な並べ方もあるみたい。こっちなんて、くねくねの曲線! 鳥が羽根を広げたような、ハロウィンのおばけのような……

これ、元の形は正方形じゃない? 曲線で、でっぱる部分と引っ込める部分を作ってる。お互いがぴったり合えば、しきつめられるんだよ。
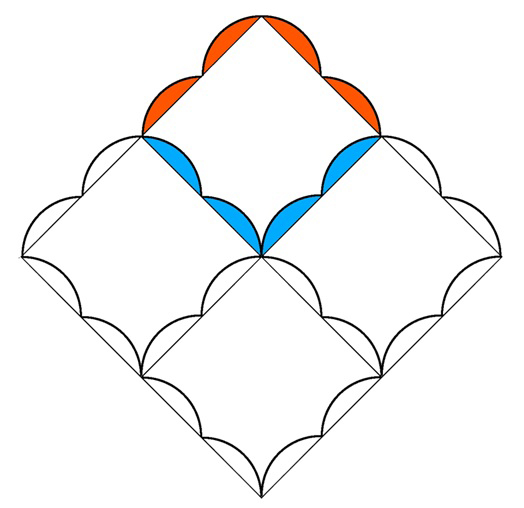
そうか、なるほど〜。じゃあ、こっちの曲線は? ちょうちんが横になったみたいな形に見えるけど……あ、わかった! これは、正六角形のしきつめの変形バージョンだ。

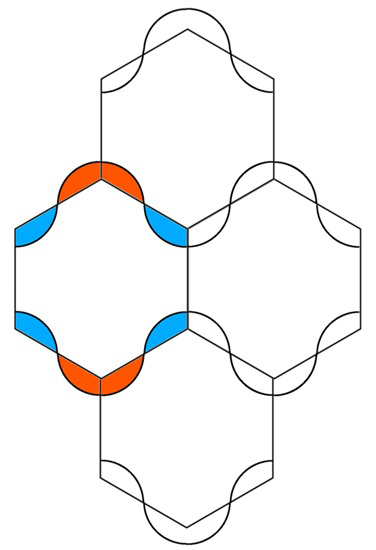
2人とも、すごいなぁ。どんどん、いいところに気がつくね。
しきつめの変形バージョン、いくらでも考えられそうだよ。
ね! いろんな形のタイルを作って並べた昔の人たち、きっとものすごく楽しかったんだろうな!
*モザイクタイルミュージアム/岐阜県多治見市。2016年開館。2006年、笠原町が多治見市に合併された際に計画が始まり、笠原町役場の跡地に建設された。建築家・藤森照信氏の設計は、タイルの原料である地元の「粘土山」がイメージされている。
*写真提供:多治見市モザイクタイルミュージアム
*イラスト作成:大野寛武
〒507-0901 岐阜県多治見市笠原町
その他のコンテンツ
