
犬吠埼
そうたです。千葉県銚子市の「犬吠埼」に来ています。ザッパーン!! って波の音が聞こえるよ。
ここは関東平野の東の端っこ、太平洋にぐっと突き出した岬だからね。すぐ近くの「九十九里浜(くじゅうくりはま)」は、東京オリンピックのサーフィン会場にもなったんだよ。
崖の上には、真っ白な灯台がある。きれいだなぁ。
登ってみようか。細くて、ぐるぐるの螺旋(らせん)階段だよ。登りながら、段数を数えてみてね。
上まで登れるんだね! ようし、数えてみるよ……10段……20段……80段……まだあるね。99段で、やっと到着。あれ? もしかして、九十九里浜だから99段?
正解! なかなか、おもしろい作りだよね。さぁ、てっぺんのここから見ると、ぐるりと海に囲まれて水平線が丸く見えるよ。
うーん、まさに絶景だ。この大きなレンズで明かりを大きくして、夜の海を照らすんだね。でもまさか、あの水平線までは届かないよね……。

*写真提供:銚子市観光協会
さて、どうかな。まずは、あの水平線までの距離を考えてみたらどう?
おもしろそうだな。図を描いてみるよ。丸い地球に、こんなふうに灯台が立ってる。
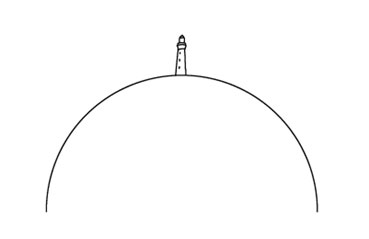
ここから照らした光が、水平線まで届くとするよ。
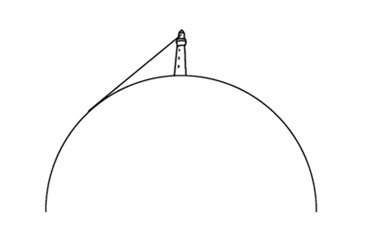
そうか。もしかしたら、三平方の定理が使えるかもしれない。どういう三角形を考えればいいのかな。
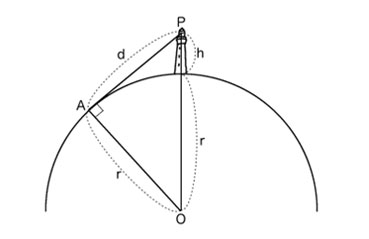
ルーロー、これはどう? 地球の中心を考えるんだ。地球の半径と、灯台の光の高さがわかれば、dの長さが計算できる!
いいね、そうたさん! 地球の半径は、6378kmくらいと考えようか。光の高さは、この灯台のデータを見ればわかりそうだ。
なるほど、そこに書いてあるね。光の高さは、水面の平均の高さから約52mだって。よし、計算してみるよ。\(\triangle\)APOは \(\angle\)OAP=90°の直角三角形だから、三平方の定理を使うと
\(d^2+r^2=(r+h)^2\)
\(d^2=r^2+2rh+h^2-r^2\)
\(d^2=2rh+h^2\)
\(d=\sqrt{h(2r+h)}\)
ここまできたら、あとは電卓で計算すればいいね。
光の高さ(h)は52mだから0.052kmで
\(0.052\times (2\times 6378+0.052)\)を計算して「\(\sqrt{ }\)」のボタンを押して……
約25.75km。
ええっ!灯台から水平線まで25km以上あるの?! この光ってそんなに遠くまで届くのかな。
いいね。ばっちりの計算だよ。そしてほら、この灯台の光が届く距離は、約36kmだと書いてある。
よかった! それなら、水平線まで十分に届く。夜になったら、今ここから見えている範囲の海のどこからでも、この灯台の光が見えるってことだ。たいしたものだね。

*写真提供:銚子市観光協会
*犬吠埼灯台/千葉県銚子市。横浜・北米航路を航行する貿易船に必要な灯台として建設され、1874(明治7)年に初点灯した。
〒288-0012 千葉県銚子市犬吠埼
その他のコンテンツ
