
明石海峡大橋
ゆうなです。ここは、兵庫県の「明石海峡大橋」。ここから見ると、支柱にケーブルが渡されていて、ずいぶん重たそうな橋が吊られているね。
この橋が開通したのは、1998年だよ。つい最近、トルコのダーダネルス海峡に世界最長の吊り橋が完成するまで、ずいぶん長い間、世界一の長さとしてギネス記録に認定されていたんだ。
世界一ではなくなったとしても、それにしても長い橋だよ。こんなに大きな橋が、ケーブルだけで吊られているなんて。切れたりしないのかな。なんだか心配になっちゃう。
支柱と支柱を結んで曲線を描いているのが、メインケーブル。これはもちろん、とんでもなく丈夫に作られているんだ。1本で3t以上の重さを支えることができる強いワイヤーを、まず127本も束ねる。これをストランドと呼んでいるんだけど、このストランドが、さらに290本も束ねられているんだって。
つまり、1本のメインケーブルは、なんと36830本ものワイヤーでできているというわけ。ちょうどそこに、ケーブルとストランドの断面図があるね。

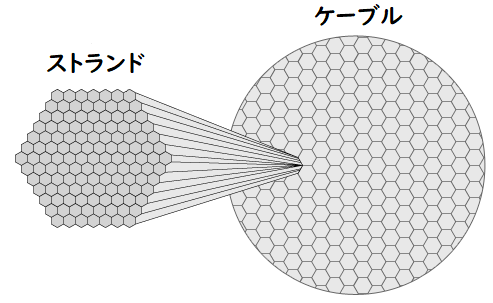
うわあ、ギチギチ、みっしり! これなら、確かに丈夫そうだね。なんだか蜂の巣みたい。
等しい大きさの円を、なるべく隙間がないように並べると、蜂の巣状になるんだ。正六角形に並ぶように、きっちり規則的にワイヤーが束ねられているね。
ふむふむ。まず、真ん中にワイヤーが1本。その周りを6本のワイヤーで囲んで、そのまた周りを12本で囲んで、またまた周りを18本で囲んでいる。規則性があるね。ええと、1本のストランドには127本のワイヤーが使われているんだっけ。いったい何層になっているのか、もしかしてこれ、計算できるんじゃない?
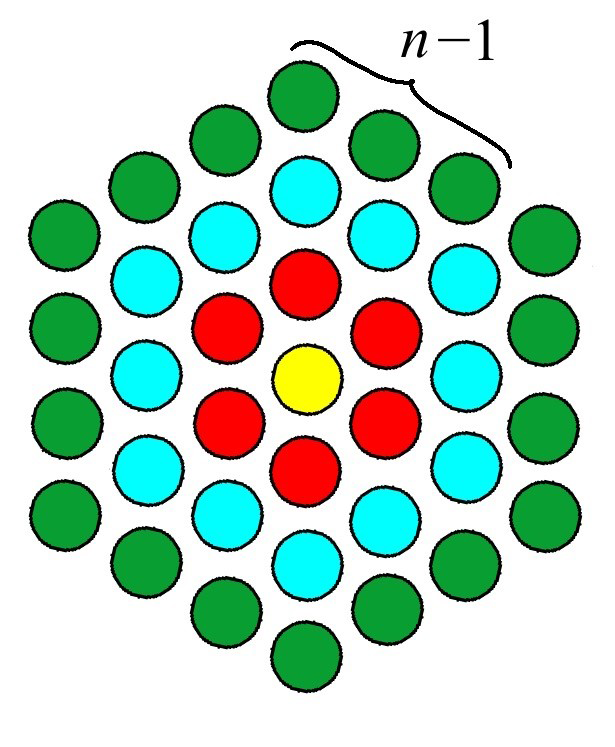
こんな感じで考えたら、どうかな。
\(n\) 層目までのワイヤーの本数は
\(1+6+12+18+・・・\)
\(=1+6\times 1+6\times 2+6\times 3+・・・+6(n-1)\)
\(=1+6 \{1+2+3+・・・+(n-1)\}\)
あれ? この後、どうしたらいいかな。
いいよ、すごくいいところまで来てるよ、ゆうなさん。
実は
\(1+2+・・・+n=\dfrac{1}{2}n(n+1)\)
が成り立つんだよ。
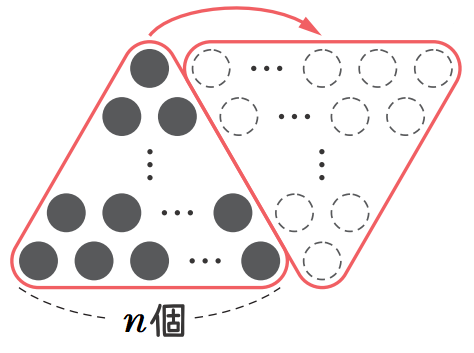
あ、なるほど! じゃあ、さっきのところから、さらに式を変形して
\(1+6\{1+2+3+・・・+(n-1)\}\)
\(=1+\dfrac{6n(n-1)}{2}\)
\(=1+3n(n-1)\)
\(n\) 層目までのワイヤーの本数は \(1+3n(n-1)\) 本になるね。
1本のストランドには127本のワイヤーが並んでいるわけだから、2次方程式 \(1+3n(n-1)=127\) を解いて
\(n=7,n=-6\)
もちろん \(n\) は正の整数だから \(n=7\)
答えは、7層目だ!
すばらしい〜! ゆうなさん、バッチリだ!!
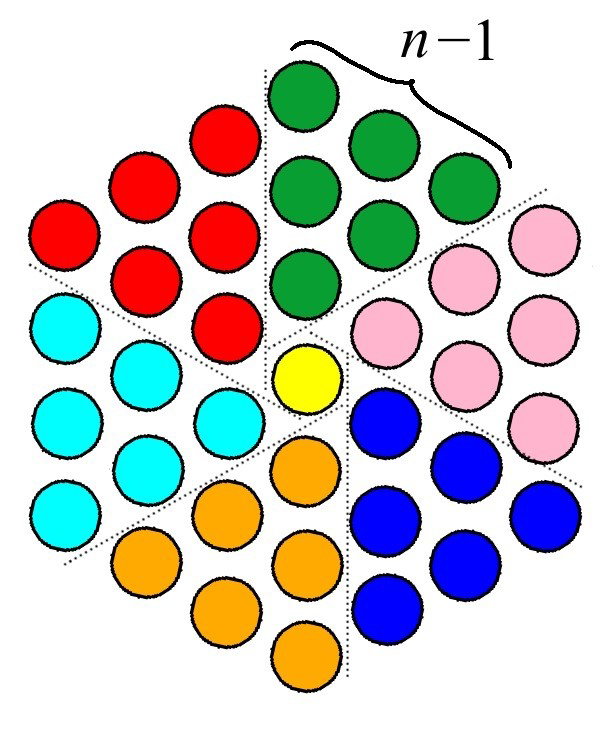
ほかにも、いろいろな見方ができるよ。たとえば、真ん中の1本のケーブルの周りを、6個の三角形が囲んでいるとかね。この場合は、どんな式になるかな。いろいろ、考えてみよう!
*明石海峡大橋/兵庫県神戸市と淡路市岩屋を結んでいる。全長3,911m、中央支間1,991m。
〒655-0047 兵庫県神戸市垂水区
その他のコンテンツ
