特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【ICT教育のイマ】クロームブック活用術 実践㊹~…
中学校
2024.01.11
【ICT教育のイマ】クロームブック活用術 実践㊹~デジタル教科書/操作編(3年 三平方の定理③)~
相模原市立相武台中学校
加藤光顕先生
今回は、3年三平方の定理の学習で活用したデジタル教科書の有効な方法をご紹介します。

①類題をこなすことで補助線を見つける感覚を養う
□単元:7章 三平方の定理 □内容:p.198 三平方の定理の利用 □学年:中学3年
教科書p.198は、平面図形(円)の中にできた線分の長さを、三平方の定理を利用して求めます。今回は円を主に扱うので、円の特徴である半径を使う場面が多くなります。前回の実践でも述べましたが、三平方の定理を利用するには、直角三角形を見いだすことが大切です。その際には、直角三角形は直角となる線分が必要であることから、その線分を構成する補助線(垂線)をひけるかがポイントとなります。前回は、座標平面としてあらかじめ直交した線がひかれていたので見つけやすかったですが、今回は線がないので、見失わないように目的をしっかりもって取り組まなくてはなりません。
このポイントを身につけるために有効なのが、シミュレーションです。問題数が1つではなく、いくつかの類題があるので、十分に練習することができます。デジタルコンテンツなので、図とともに問題を滞りなく提示させることができ、生徒も考えやすく準備の手間もかかりません。この類題をこなすことで、直角三角形を見いだすポイントとなる補助線(垂線)を自分でひく感覚を養うことができるようになります。


②シミュレーションで奥行きを捉えながら、底面との関係や直角三角形を見いだす感覚を養う
□単元:7章 三平方の定理 □内容:p.199 三平方の定理の利用 □学年:中学3年
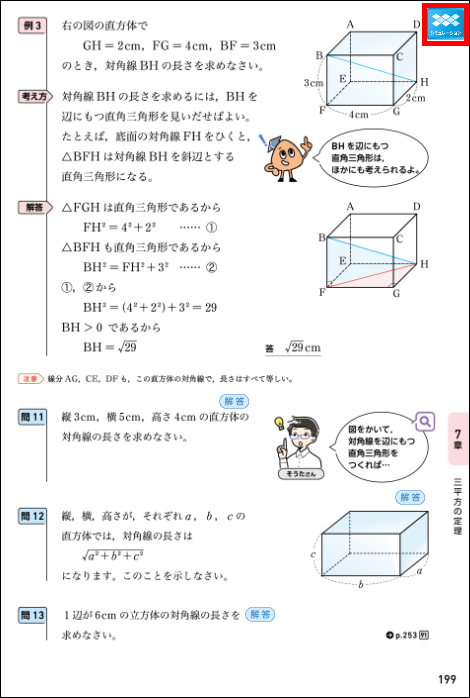
教科書p.199は、内容が前回の実践で扱った平面図形から空間図形へと変わって、直方体の対角線を三平方の定理を利用して求めます。例題にある直方体の対角線 \(\text{BH}\) を求めるためには、まずその対角線が斜辺となる直角三角形 \(\text{BFH}\) を見いだす必要があり、さらに斜辺を求めるために残りの2辺 \(\text{BF}\) と \(\text{FH}\) を求めなければなりません。\(\text{BF}\) は直方体の高さなので容易に求めることができますが、 \(\text{FH}\) は一見長さがわかりません。この際、\(\text{FH}\) が底面(長方形)の対角線であることに気づくことが重要となります。これに気づけば、三平方の定理を利用してまず長方形の対角線 \(\text{FH}\) を求め、その長さを使ってさらに\(\triangle \text{BFH}\)でも三平方の定理を利用することで、直方体の対角線 \(\text{BH}\) を求めることができます。
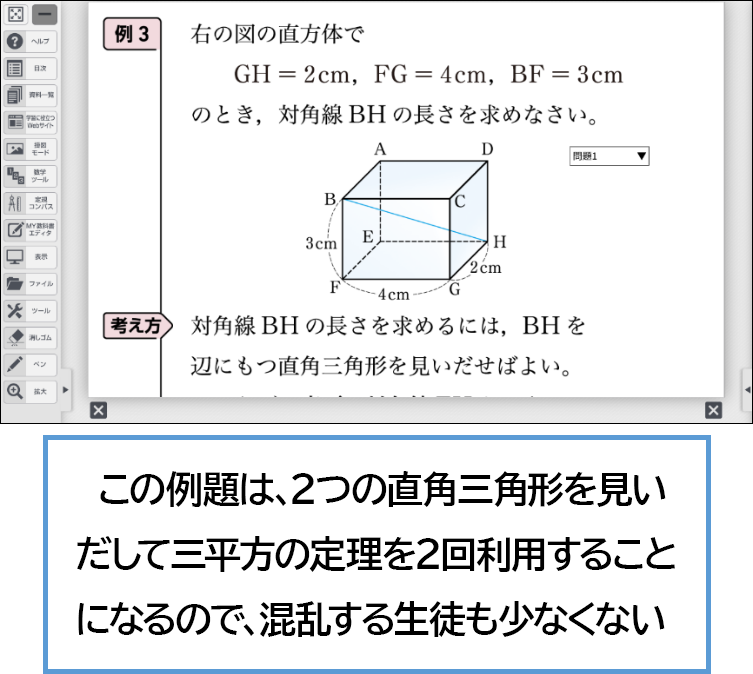
この例題は、2つの直角三角形を見いだして三平方の定理を2回利用することになるので、混乱する生徒も少なくありません。後に、直方体の縦、横、高さをそれぞれ \(a\)、\(b\)、\(c\) とすると、直方体の対角線の長さは、\(\sqrt{a^2+\ b^2+\ c^2}\) となることを学びますが、その前にこの例題をしっかりと理解しておく必要があります。
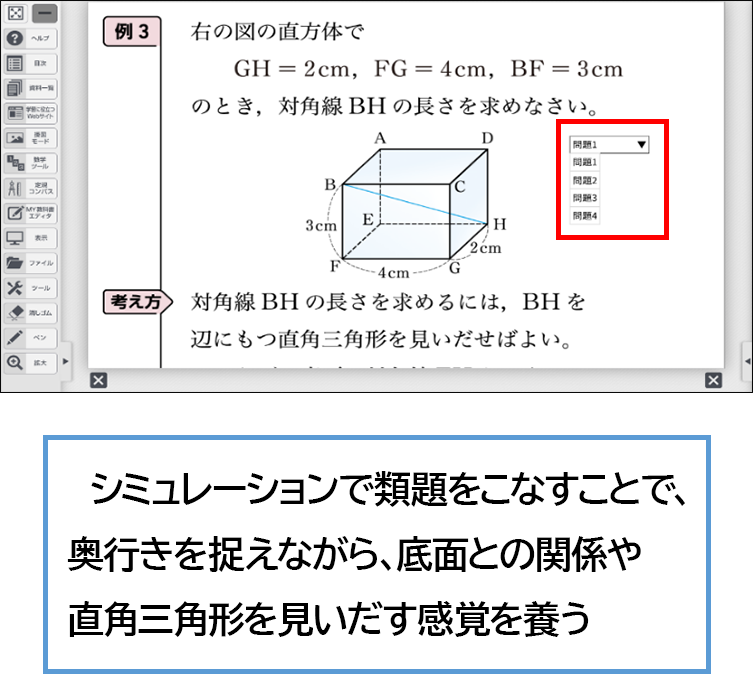
そこで有効なのが、シミュレーションです。何種類か類題を提示できるので、何度も練習することができます。デジタルコンテンツなので、図とともに問題を滞ることなく提示させることができ、生徒も考えやすく、問題を準備する手間もかかりません。この類題をこなすことで、混乱していた生徒も徐々に理解することができました。このような空間図形において、奥行きを捉えながら、底面との関係や直角三角形を見いだす感覚を養うことができたのだと思います。
その他のコンテンツ
