中学校
2023.12.14
【ICT教育のイマ】クロームブック活用術 実践㊵～デジタル教科書／操作編（3年 三平方の定理①）～
相模原市立相武台中学校
加藤光顕先生
今回は、3年三平方の定理の学習で活用したデジタル教科書の有効な方法をご紹介します。
①デジタルコンテンツで図の提示がより便利に
□単元：7章 三平方の定理 □内容：p.186 三平方の定理の導入 □学年：中学3年
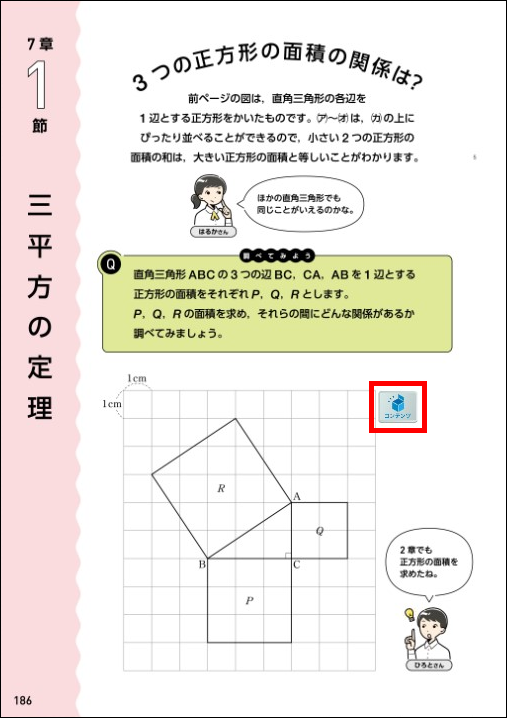
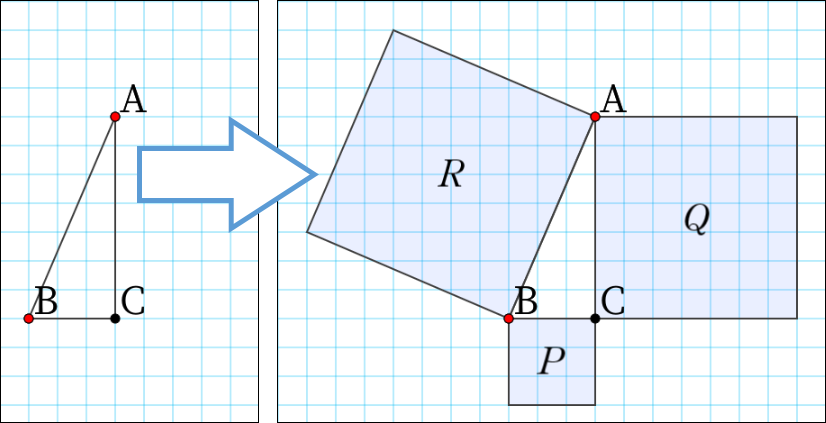
前回の実践で、教科書p.185の（ア）～（オ）を組み合わせると、（カ）の上にぴったり並べることができることを確認しました。今回はさらに数学的に、値を使って面積の和を式に表していく内容となります。図にもあるように、直角三角形 \(\text{ABC}\) の3つの辺 \(\text{BC}\)、\(\text{CA}\)、\(\text{AB}\) を1辺とする正方形の面積をそれぞれ \(P\)、\(Q\)、\(R\) とし、それらの面積の関係を調べていきます。
まずは例題として、図にかかれている図形を考えさせます。方眼を利用すれば、\(P\) と \(Q\) の面積は1辺を2乗すればよいので容易に求めることができますが、\(R\) の面積は同様に求めることはできません。苦戦する生徒もいると思われるので、そのようなときは全体で確認します。\(R\) の面積を求める解法を思いつく生徒は必ずいますが、その生徒に説明させることで、苦戦していた生徒も質問を繰り返しながらわかるようになっていきます。
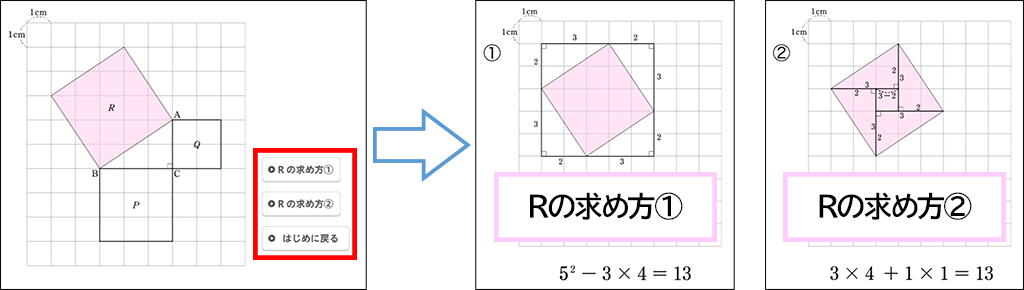
生徒に説明させる際に便利なのが、デジタルコンテンツのアニメーションです。求めたい面積に色が塗られ、さらに数値と式も表示されるのでとてもわかりやすいです。また2通りの求め方を示せるので、解法を思いついていた生徒にも、思いつかなかった生徒にも、思考の整理や広がりのきっかけとなるでしょう。
②デジタルコンテンツならドラッグとクリックだけで、簡単に図形がかける
□単元：7章 三平方の定理 □内容：p.187 三平方の定理の導入 □学年：中学3年
教科書p.186で面積の求め方を確認したあとは、今度は自分で直角三角形を決めて、その各辺を1辺とする正方形を考えます。これらの正方形を \(P\)、\(Q\)、\(R\) とし、面積の関係を調べていきますが、いろいろな大きさの直角三角形をかかせることで、その特徴の一貫性に気づきやすくなるはずです。
例えば、\(\text{BC}=3\text{cm}\)、\(\text{CA}=7\text{cm}\) の直角三角形ならば、\(P=3^2=9\text{cm}^2\)、\(Q=7^2=49\text{cm}^2\)、\(R=10^2-3 \times 14=58\text{cm}^2\)となります。
このように、いくつかの直角三角形から \(P\)、\(Q\)、\(R\) を表にまとめると、
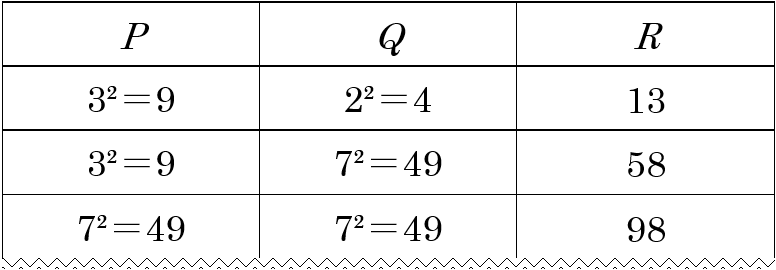
となり、どのような場合でも \(P+Q=R\) になることが予想できます。また、正方形の面積であるため辺の2乗になること、その辺は直角三角形の辺の長さによって決まることを印象づけるため、指数を残しました。
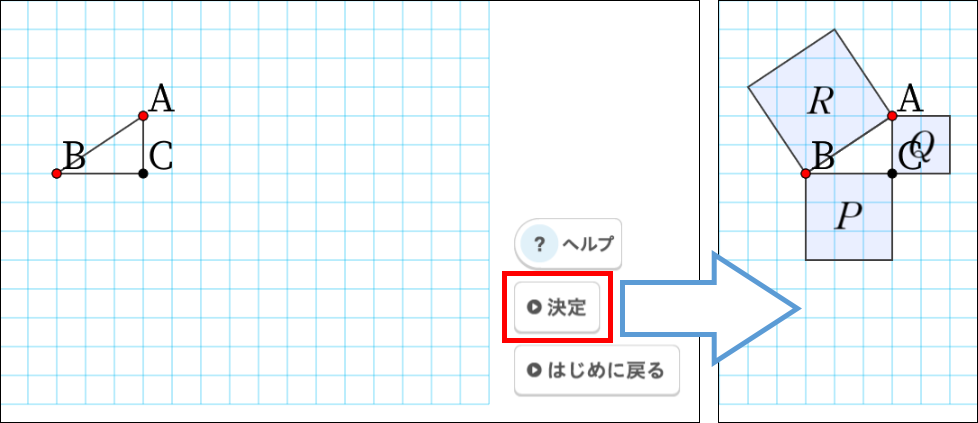
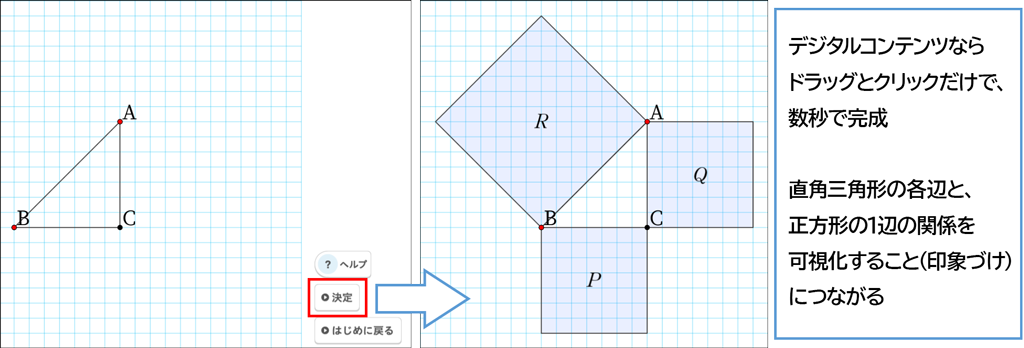
正方形を示す際、デジタルコンテンツのシミュレーションを用いれば、直角三角形を指定して決定ボタンを押すだけで、簡単に表示することができて非常に便利です。生徒にさまざまな直角三角形を確認させたくても、手描きだとどうしても時間がかかってしまいます。しかし、デジタルコンテンツならドラッグとクリックだけで数秒で完成するので、確認の際に大変有効です。
その他のコンテンツ