特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【ICT教育のイマ】クロームブック活用術 実践⑩~…
中学校
2022.06.29
【ICT教育のイマ】クロームブック活用術 実践⑩~プログラミング/新学習指導要領編~
相模原市立相武台中学校
加藤光顕先生
今回は、新学習指導要領を意識して、論理的思考力を推進するための教材となるプログラミング(Scratch)を活用した授業の2回目をご紹介します。

①代入と式の値がプログラミング(コーディング)の基礎となる。
□単元:1章 式の計算 □内容:教科書p.19の式の値 □学年:中学2年生
教科書p.19問7には、式の値を求める問題があります。式の値については、1年生の既習事項となりますが、2年生ではさらに文字が1種類増える2元1次式となることで問題解決の範囲を広げることができるわけです。このときにScratchで計算ソフトを作らせる取り組みを入れることで、値を代入し、式の値を求める考え方やその良さについて、体験的に学ぶことができます。
課題1復習 式の値とは何か、\(5a+2\) と \(a=-2\) を使って説明しなさい。
課題1の考え方
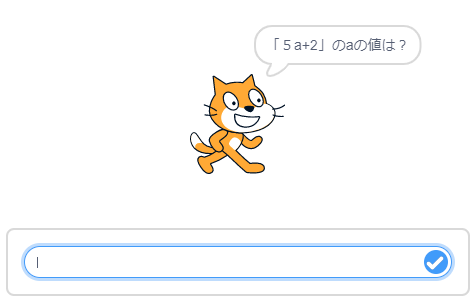
<コードの流れ>
- ① \(5a+2\) の \(a\) の値をきく。
- ② \(a\) の値を代入した演算の式で計算する。
- ③ 計算した値を言う。
<使うコマンド>
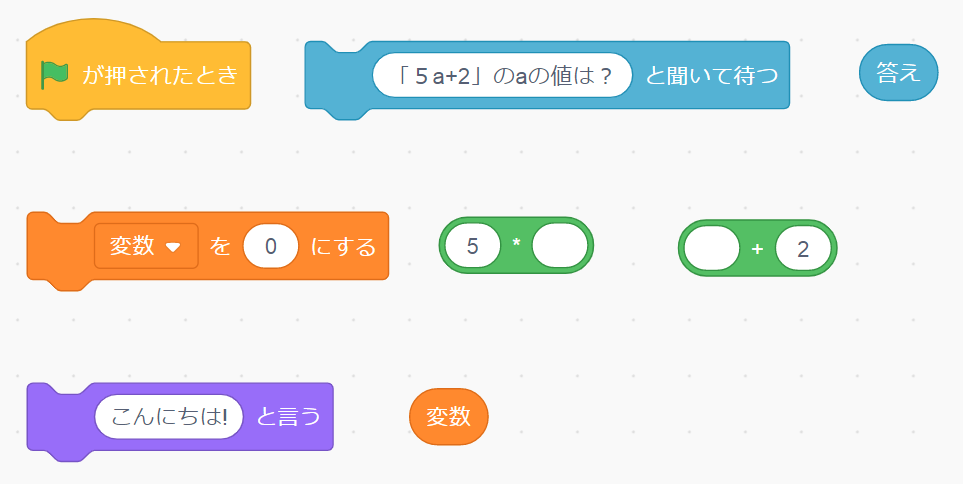
課題2 \(a=-2\)、\(b=\frac{1}{3}\) のとき、\(4(a+2b)+(a-5b)\) の式の値を求めなさい。
課題2の考え方
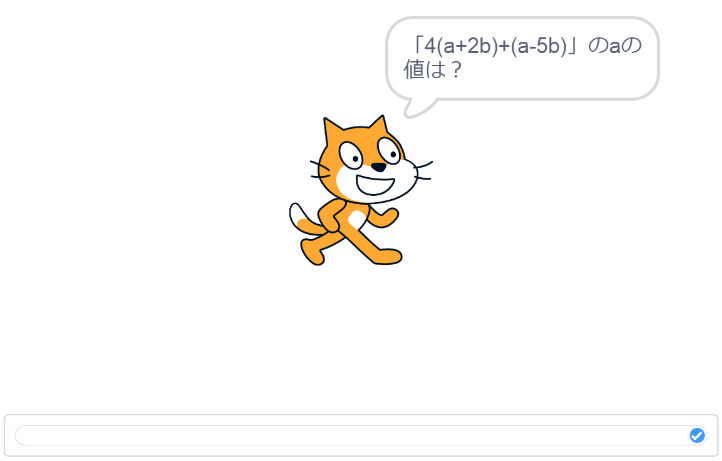
<コードの流れ>
- ① \(a=-2\) の \(a\) の値をきく。
- ② \(a\) の値を代入した演算の式で計算する。
- ③ \(b=\frac{1}{3}\) の \(b\) の値をきく。
- ④ \(b\) の値を代入した演算の式で計算し、その値だけ変える。
- ⑤ 計算した値を言う。
<使うコマンド>

②解法の違い(考え方の違い)を共有することで理解を深める。
次の解法1から3は、実際に生徒が作ったコードです。コードは、計算の途中式と同様で考え方の違いを発見することができます。スモールステップで考えていくことで、それぞれの考え方の共通点や良さを考えさせることで代入と式の値について理解を深めることができました。また、こうした機会は、プログラミングのアルゴリズムを今後考えていくうえでも必要不可欠だと思います。
[注意]Scratchでは分数の入力が難しいので、\(b\) の値を入力するときは、0.333を用いると良い。
〇解法1(文字式の同類項をまとめてから値を代入する方法)

※Scratchはこちら https://scratch.mit.edu/projects/702707912/
〇解法2(はじめの文字式に \(a\) と \(b\) の値を代入する方法)
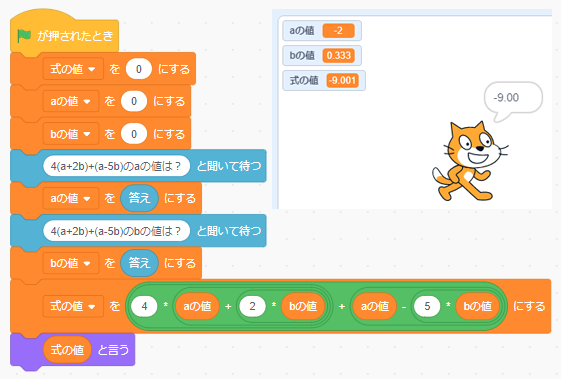
※Scratchはこちら https://scratch.mit.edu/projects/702709425/
〇解法3( \(A=a+2b\)、\(B=a-5b\)として、\(A\)と\(B\)の値を求めてから式の値を求める方法)
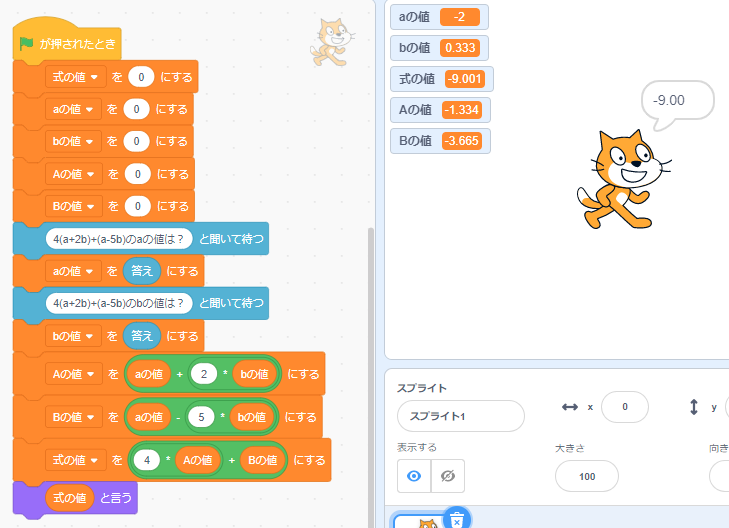
※Scratchはこちら https://scratch.mit.edu/projects/702709889/
③まとめ
以前も記載しましたが、Scratchの良さは、次の点です。
- ○何度もやり直しができること
- ○コードを間違えていると、正しく実行しないこと
- ○自分で応用できること
- ○コーディングが、数学的思考力を養う過程に繋がること
うまく実行されない場合、「なぜ、うまくいかないのか」を考え、配置を変えたりして実行します。うまく実行できた場合、今度は「なぜ、うまくいったのだろう」と考えます。また、「なぜこのコマンド(ブロック)が必要なのか」を考えることもコードの理解には不可欠です。このような過程を通して、コーディングを理解していくのだと思います。コーディングは、数式をスモールステップで解く手順と同じだと感じた生徒も多くいました。
プログラミング的思考は、情報化社会を生きるうえで一層大切な力として小学校から必修化されており、ゲームなどにも組み込まれているので、生徒が身近に感じる教材の1つです。中学校でも技術の授業だけでなく、数学の授業でも積極的に活用することで、数学への関心や思考力を高める一助となるはずです。
その他のコンテンツ
