今日の授業のひと工夫（小中学校）

5年第4単元「小数のかけ算」では、乗数が小数の乗法を学習します。

乗数が整数の場合は、乗法は同数累加の意味で捉えることができますが、乗数が小数になると同数累加の意味では捉えることはできません。
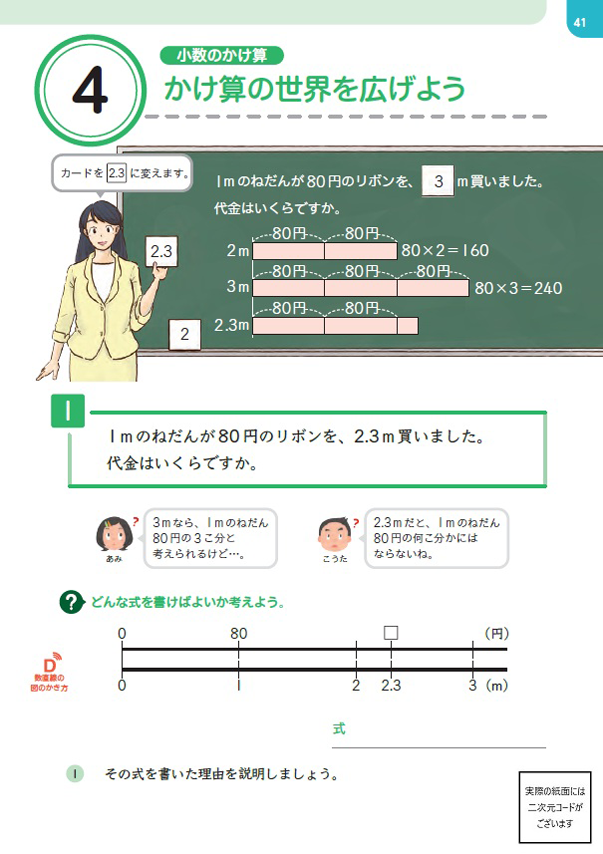
例えば、5上p.41の場面では、あみの吹き出しのように、リボンの長さが \(3\)mであれば、「\(80\times 3\) は \(80\) 円の \(3\) こ分（\(80+80+80\)）」と考えられます。
しかし、乗数が小数（\(80\times 2.3\)）の場合は、「\(80\) 円を \(2.3\) 回たす」という考えはできません。 ここで、乗法の意味の拡張が必要になります。

▲新しい算数5上 p.41～42

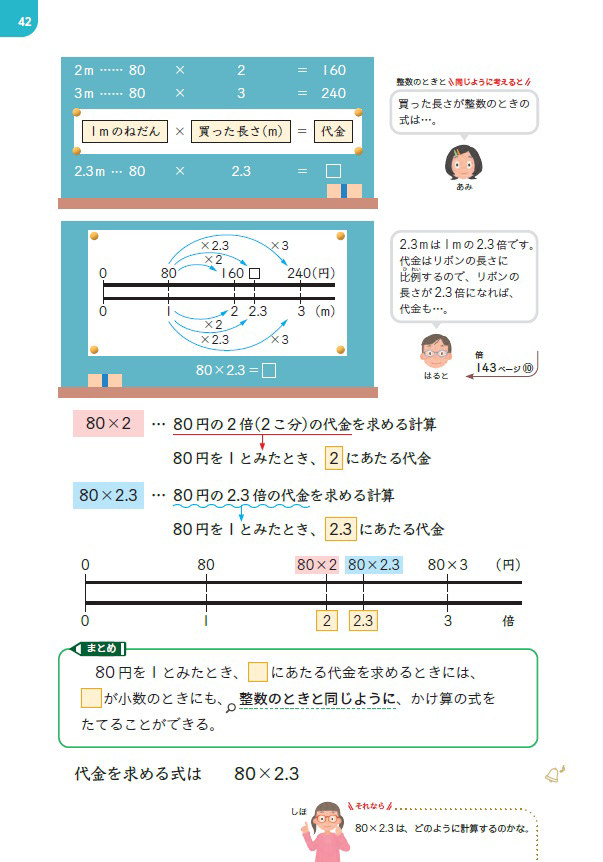
5上p.42のあみ、はるとのように、言葉の式や比例の考えを使って立式した後、\(\boldsymbol{80\times 2.3}\) は、「\(\boldsymbol{80}\) 円を \(\boldsymbol{1}\) とみたとき、\(\boldsymbol{2.3}\) にあたる代金を求める計算」であることを、数直線を活用しておさえていきましょう。

この割合の見方をおさえることで、乗法の意味を拡張します。割合の見方は、4年「倍の見方」単元や4年第13単元「小数のかけ算とわり算」内での小数倍、5年第3単元「比例」の第3時で、繰り返し扱ってきています。

まとめでは、乗数が小数の場合も、整数の場合と同じように考え、乗法の意味を統合的に捉え直したことをていねいに振り返りましょう。