今日の授業のひと工夫（小中学校）

3下p.51では、2mの\(\dfrac{3}{4}\)の長さの表し方を考えることを通して、\(\dfrac{3}{4}\)m（量分数）と基準量の\(\dfrac{3}{4}\)（分割分数）の違いを理解していきます。

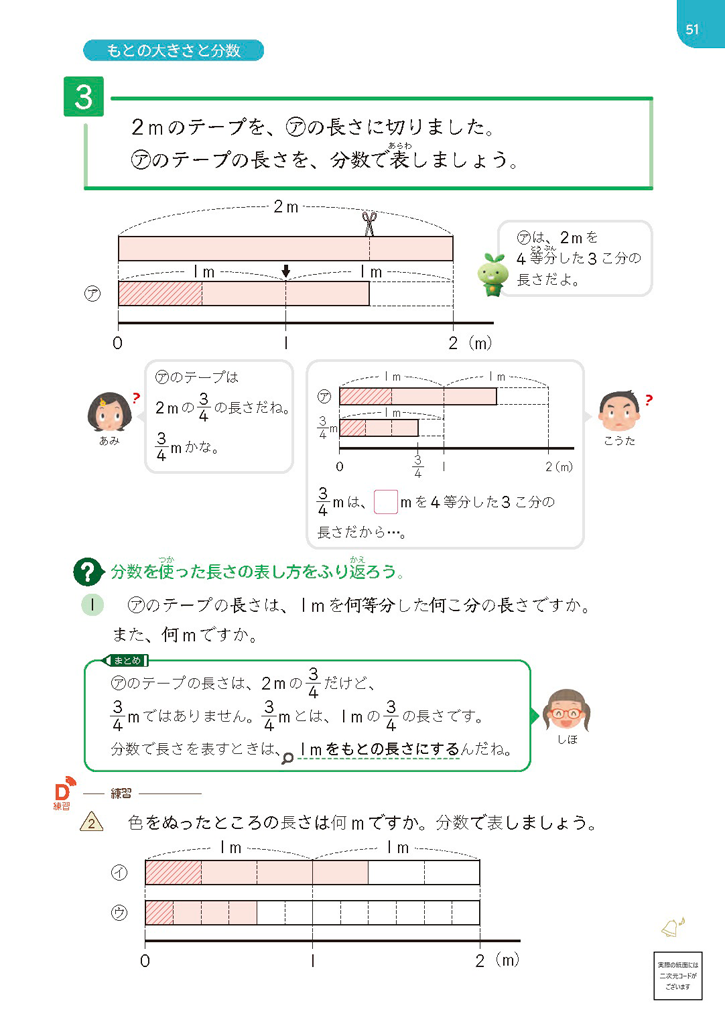
㋐のテープを見て、「2mの\(\dfrac{3}{4}\)の長さは、\(\dfrac{3}{4}\)m」と考えてしまう児童は多くいます。しかし、本単元で学習してきたように、\(\dfrac{3}{4}\)mというのは、1mを4等分した3こ分の長さを表しています。分数で長さを表すときは、基準量を1mにすることをあらためて確認していきましょう。

教科書の吹き出しや補助発問に沿って、

• ㋐は、2mの\(\dfrac{3}{4}\)の長さ
• ㋐は、1mを2等分した3こ分の長さ
• ㋐は、\(\dfrac{1}{2}\)mの3こ分なので\(\dfrac{3}{2}\)m

というように、段階的にポイントをおさえて指導することで、「㋐は、2mの\(\dfrac{3}{4}\)だけど、\(\dfrac{3}{4}\)mではない」ことを理解させます。

単元末「つないでいこう算数の目」では、基準量に着目して、分数を使って大きさを表したことを振り返ります。本単元の学習を通して、基準量が1mや1Lなどの大きさを等分して、大きさを表すことをしっかりと理解させたいですね。