今日の授業のひと工夫（小中学校）

5上p.112では、分数倍について学習していきます。児童は、5上p.64からの「小数の倍」単元で小数倍について学習してきていますので、既習事項をもとに、分数倍の意味を考えさせたいですね。

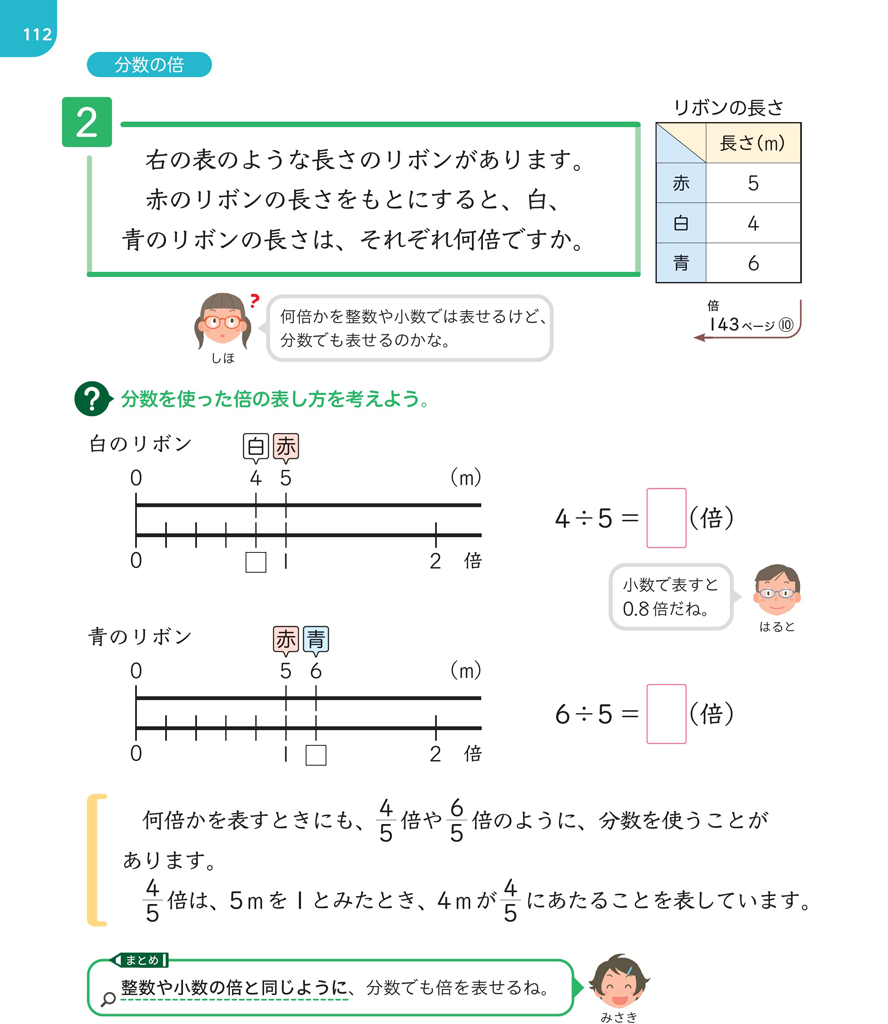
まず、赤のリボンの長さをもとにすると、白のリボンの長さは何倍になるかを考えます。数直線を見て立式すると、\(4 \div 5 = \dfrac{4}{5}\) で、\(\dfrac{4}{5}\) 倍となります。このとき、商を小数で表すと \(0.8\) になり、小数倍では \(0.8\) 倍と表せることをおさえましょう。

次に、赤のリボンの長さをもとにすると、青のリボンの長さは何倍になるかを考えます。こちらも同様に、分数倍では \(\dfrac{6}{5}\) 倍、小数倍では \(1.2\) 倍と表せます。

このことを踏まえて、整数倍や小数倍と同じように、分数でも倍を表せることをまとめていきましょう。 「基準量を1とみたときに、比較量が○にあたる」という倍の意味は、5年下で学習する割合の理解につながっていきます。本時では、教師は割合の学習を見据えて、分数倍の意味を、整数倍や小数倍の意味と統合的にとらえさせたいですね。