今日の授業のひと工夫（小中学校）

6年p.121では、半径10cmの円の面積の求め方を考えます。

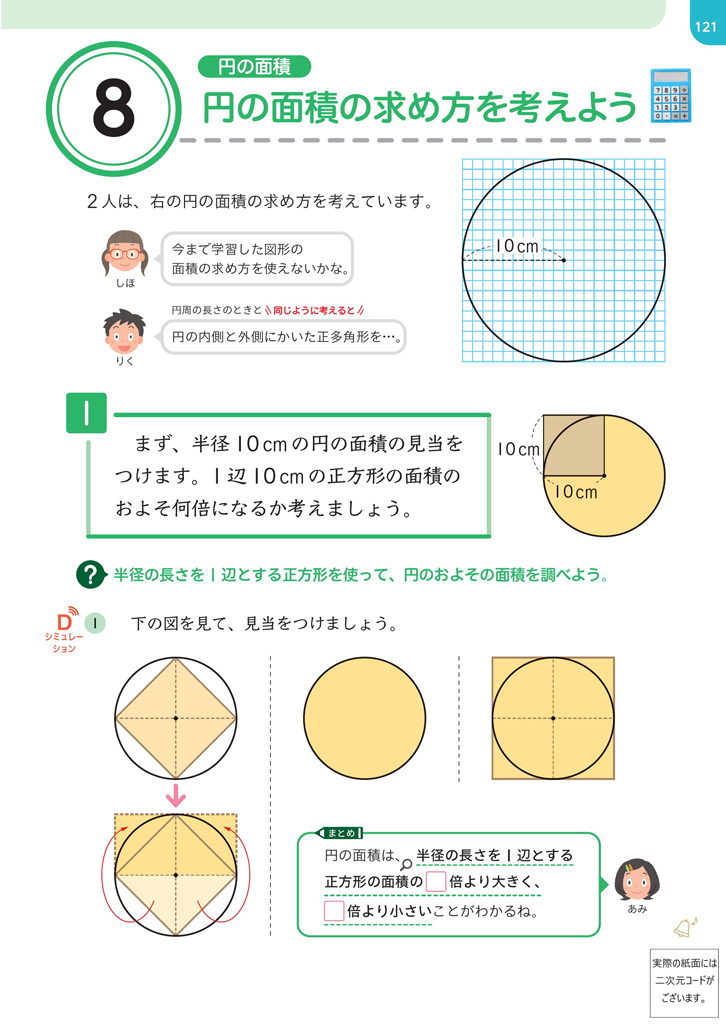
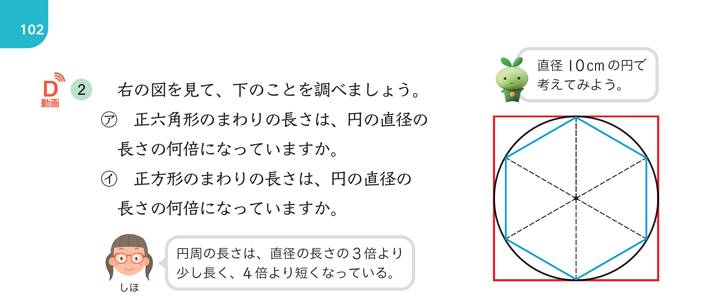
りくの吹き出しをヒントに、5年で円周の長さの見当をつけるときに、円に内接する正六角形の周より長く、円に外接する正方形の周より短いと考えたことを想起させましょう。この時と同じように考えて、円に内接する正方形と、外接する正方形を使って、円の面積の見当をつけます。

\(\boxed{\ 1\ }\)では、半径10cmの円の面積が、1辺10cmの正方形の面積のおよそ何倍になるかを考えます。ここで、円の半径と正方形の1辺の長さが同じであることをおさえておきましょう。

円に内接する正方形では、下半分の三角形を上側に移動させると、1辺10cmの正方形が2つできるので、面積が2倍であることがわかります。
円に外接する正方形については、1辺10cmの正方形の4倍の面積であることは、教科書の図を見てすぐに理解できるでしょう。
理解が難しい児童には、教科書のQRコンテンツを使って、確認させてもよいでしょう。

これらのことから、円の面積は、半径の長さを1辺とする正方形の面積の2倍より大きく、4倍より小さいので、約3倍という見通しをもたせます。
授業の最後には、もっと詳しく調べたいという新たな問いを児童から引き出し、次時につなげたいですね。