今日の授業のひと工夫（小中学校）

「新編 新しい数学」2年p.25～26では、次のQについて考えます。

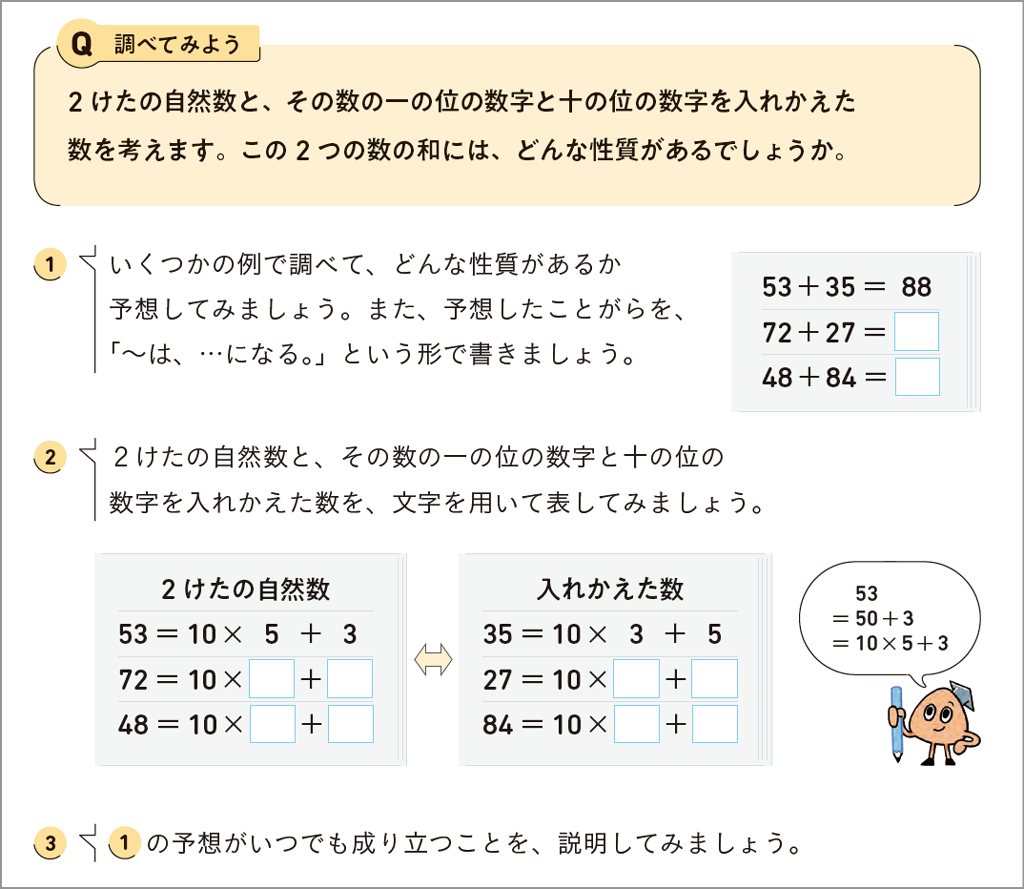
p.26④では、数の性質について条件を変えるとどんなことがわかるかを考えます。りおさんの吹き出しにあるように「2けたを3けたにする」や「和を差、積、商にする」などの条件変えを生徒が豊かに発想できるように意識したいところです。こうした経験を積み重ねて、生徒の問題の見方がより豊かになっていきます。

ここでは、りおさんの吹き出しにある「『2けた』を『3けた』に変えた場合」について考えてみましょう。

まず、2けたの自然数の表し方から3けたの自然数を \(100a+10b+c\) と表します。ここから \(100c+10b+a\) をひくと、 \(99a-99c\) となります。このあと、どのように変形するかを考えます。

変形の1つとして、\(9(11a-11c)\) が考えられますが、\(11a-11c\) が整数であることをいうために \(9 \times 11(a-c)\) と変形する考え方もあります。この式変形から、\(a\)、\(c\) が1桁の自然数だから \(a-c\) が整数であることが明確になりますね。

このように、説明したことがらから新たな性質を発見するには、説明で使った式、特に、変形したあとの式に注目することが大切です。はじめの式変形で、\(9 \times 11(a-c)\) に注目すれば、11の倍数や99の倍数になることや、百の位の数と一の位の数の差の9倍や11 倍になることもわかりますね。

このように変形した式をふり返ることで、新たな発見ができるよさを生徒に伝えたいですね。

関連記事はこちら

＞【2年1章】式による証明