今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年1章3節「式の計算の利用」では、乗法公式や因数分解の公式を利用して、数の計算の結果や式の値をくふうして求めたり、数の性質が成り立つことを文字を使って証明したりします。また、図形の性質が成り立つことを、文字式とその計算を利用して証明します。
それらの証明の学習を通して、証明しようとしていることがらを意識して、目的に応じて式変形する必要があることを、生徒が意識できるようにしています。

p.34⑥では「2つの続いた奇数の積に1を加えた数」という1つの式について、④と⑤で「4の倍数になる」「ある数を2乗した数になる」という異なる結論が得られたことをふり返るようにしています。

p.34下部にある「大切にしたい見方・考え方」では、目的に応じて式変形することについてイラストとともに紹介しているので、ふり返りの際に活用してみてください。

また、p.39 章の問題B \(\boxed{\ 5\ }\) では、一の位が5である2けたの自然数の2乗の計算について、あおいさんが考えた計算方法が正しいことを証明する問題を取りあげています。

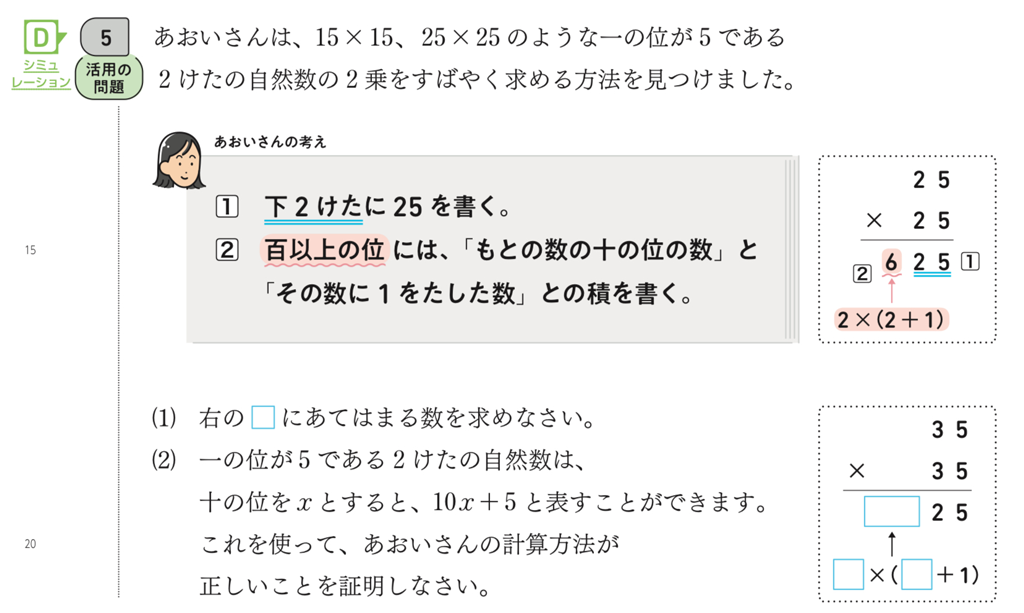
一の位が5である2けたの自然数を \(10x+5\) と表すと、2乗した数は \(100x^2+100x+25\) となります。この式を \(100(x^2+x)+25\) と変形することで、あおいさんが考えた方法が正しいことを証明できます。しかし、\(25(4x^2+4x+1)\) と変形してしまうと、下2けたが25になることが見えづらくなり、百以上の位の説明もできなくなってしまいます。
このように、目的に応じて式変形することをより意識できる問題となっていますので、生徒の実態に合わせて授業で扱ってみてください。

関連記事はこちら

＞【思考を見せる板書例】3年1章：2つの連続する奇数の積に1を加えると4の倍数になる？