今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年8章p.218では、p.217の活動の結果を箱ひげ図に表します。

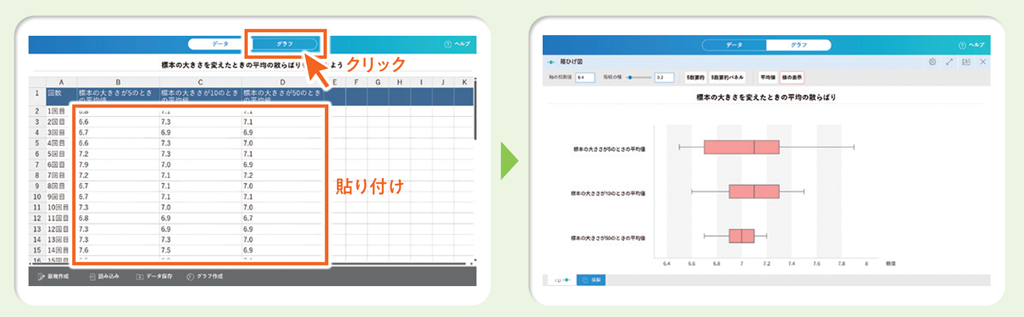
QRコンテンツを使うことで、自分で調べた結果を簡単に箱ひげ図に表すことができます。

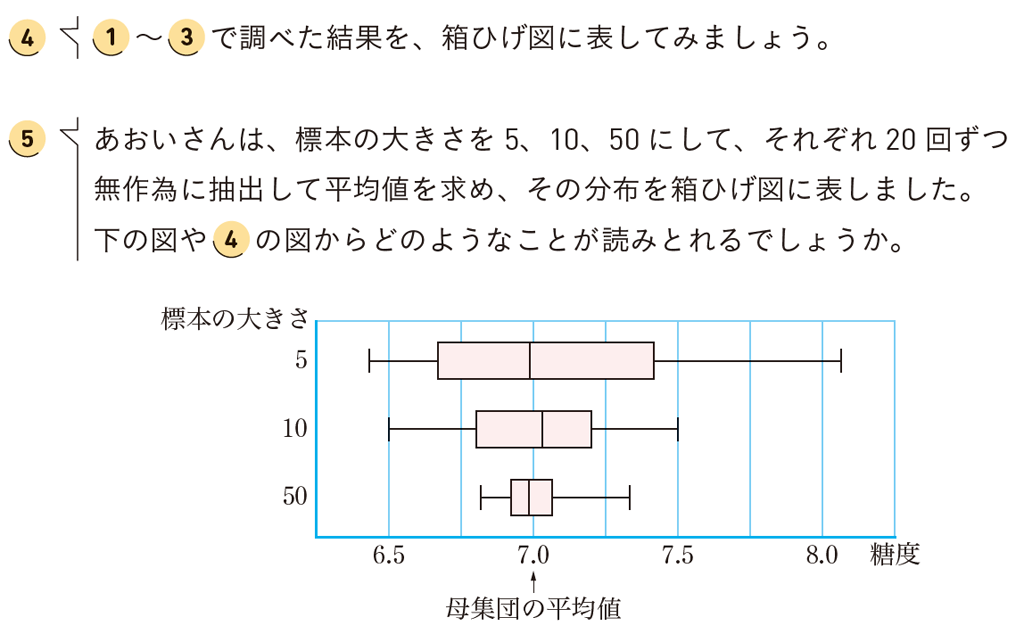
標本の大きさを大きくすれば、データの数が母集団に近づくため、標本平均のばらつきは小さくなり、母平均に近づきます。これは、標本調査が全数調査に近づくことを意味していますね。

しかし、精度が上がるからといって、できるだけ多くの標本を取り出せばよいということではありません。標本調査の意義や必要性にもう一度立ち返り、なるべく少ない労力で、なるべく信頼できる値を推定したいという目的の下で、標本の大きさを適切に決める必要があることに気づかせたいところです。

ゆうまさんとはるきさんの会話にあるように、母集団の縮図として適切な標本をつくるためには、どのくらいの標本の大きさにすればよいのかという疑問が生徒から出てくるでしょう。

数学的には、母集団の統計量をもとに、ある信頼度において標本の大きさを少なくともどれぐらいにすればよいかを求めることができます（高等学校の数学Bで学習します）。しかし、実際には、母集団の統計量がわからないことも少なくありません。したがって、一般には、過去の類似の調査等をもとにして、状況に応じて標本の大きさを設定していることが多くあります。

QRコンテンツはこちら

＞標本の大きさを変えたときの平均値の散らばりを見てみよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。