今日の授業のひと工夫（小中学校）

「新しい数学」3年3章p.83Qでは、2次方程式をこれまでに学んだいろいろな方法で解き、それぞれの解き方をふり返り、それぞれのよさを見いだすことをねらいとしています。

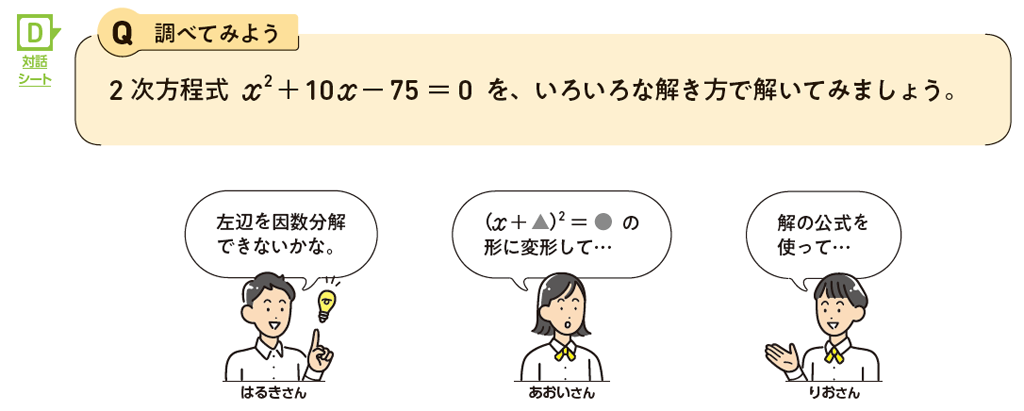
Qの2次方程式 \(x^2+10x-75=0\) は、上の吹き出しのように、3つの解き方が考えられます。まず、生徒に自由に考えさせたいですね。生徒の考えを取り上げて、3つの解き方を板書し比較します。単に比較するだけでなく、それぞれのよさを明らかにしたいところです。このことを通して、2次方程式の解き方を選ぶ観点を生徒が自覚できるようになっていきます。
簡単に因数分解ができるものであれば、因数分解する方法がもっとも時間がかかりません。一方で、解の公式はどんな2次方程式でも解けるというよさはありますが、係数によっては値が大きくなり計算が複雑になる可能性があります。ですが、この場合、\(x\) の係数が偶数であれば \((x+▲)^2=● \) の形に変形する解き方のほうが容易に解くことができます。
これらの観点を、生徒が実感を持って見いだせるとよいですね。
必要に応じてp.76、p.79、p.81 をふり返りながら、2次方程式の解き方を確認するとよいですね。
また、どの解き方でも解が同じになることを確認したいところです。

問1では、Qでの活動をふり返り、その解き方を選んだ理由も答えます。例えば、⑶ のように、\(x\) の係数が偶数でなおかつ大きく、解の公式の計算が容易でないときには、平方の形に変形する解き方が有効ですね。今後は、いろいろな2次方程式が混在して出てきます。そうたさんの吹き出しにもあるように、方程式のどの要素に着目して解法を選んだのかを確認しておきたいところですね。2次方程式を適当な方法で解くことができるようになりたいですね。

関連記事はこちら

＞【思考を見せる板書例】3年3章：いろいろな2次方程式