今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年巻末p.266「黄金比」では、縦と横の比についてさらに考えを深めていきます。p.63で調べたコピー用紙の縦と横の比と、新書判やICカードの縦と横の比は異なっています。ここでは、その比について考えるなかで、相似や2次方程式が活用できることに気づかせたいところです。また、このような数理的な考え方が人間の文化と深くかかわっていることも感じさせたいですね。

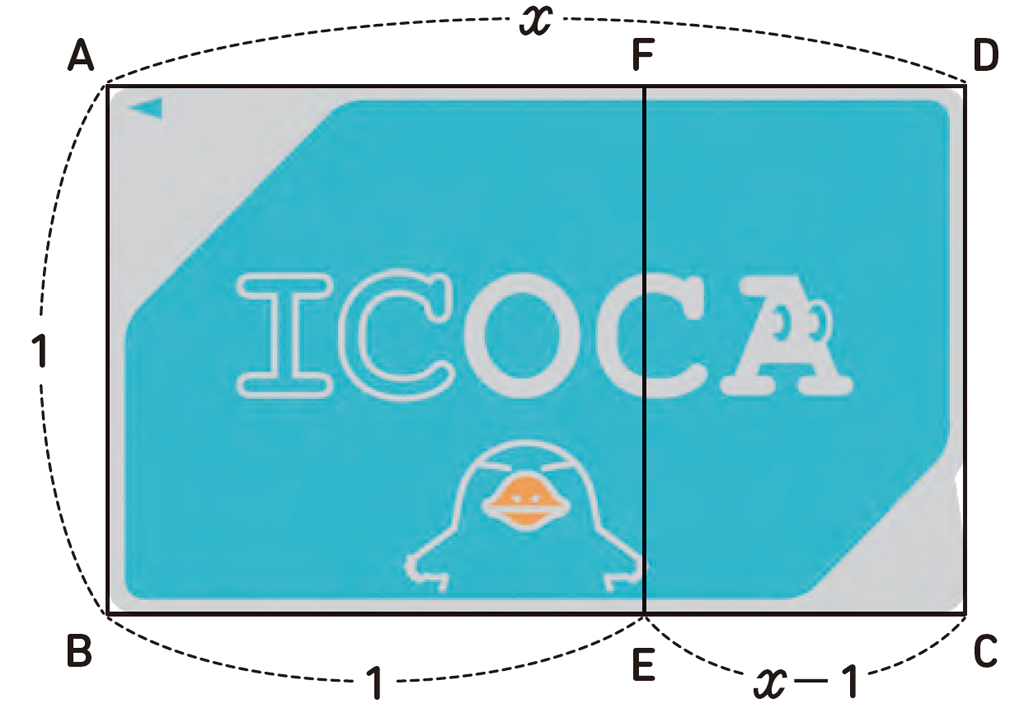
上のような長方形を黄金長方形といい、昔のギリシャの人々は長方形のなかでもっとも美しい形と考えたといわれています。授業では、次のような長方形の紙を黒板にはり、どれがもっとも美しい長方形だと思うか聞いてみるとおもしろいかもしれません。

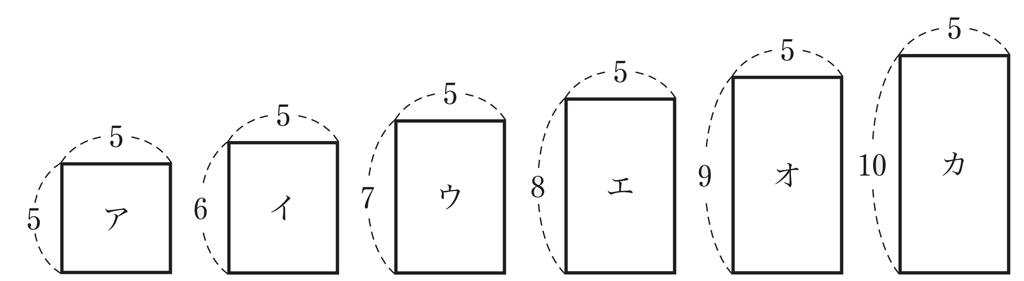
ウが \(1:\sqrt{2}\) の長方形（白銀長方形）に近く、エが黄金長方形に近い。

もちろん美しさの基準は人により異なるので正解はないのですが、それを通して古代ギリシャの人々の美意識を考えることも楽しみたいですね。

②では、正五角形のなかの黄金比を見つけます。正五角形の1つの頂角は \(540^{\circ}\div 5=108^{\circ}\)であり、\(\triangle\mathrm{ABE}\) は二等辺三角形であることから、\(\angle\mathrm{ABE}=36^{\circ}\) を導くことができますね。
また、円周角の定理を用いて、●の角はすべて等しいことを示すこともできます。 今まで学んだことを活用して多様な見方をしたいところですね。