今日の授業のひと工夫（小中学校）

「新編 新しい数学」1年1章p.29では、移動と正の数の範囲での加法をもとに、正負の数の加法を考えることをねらいとしています。

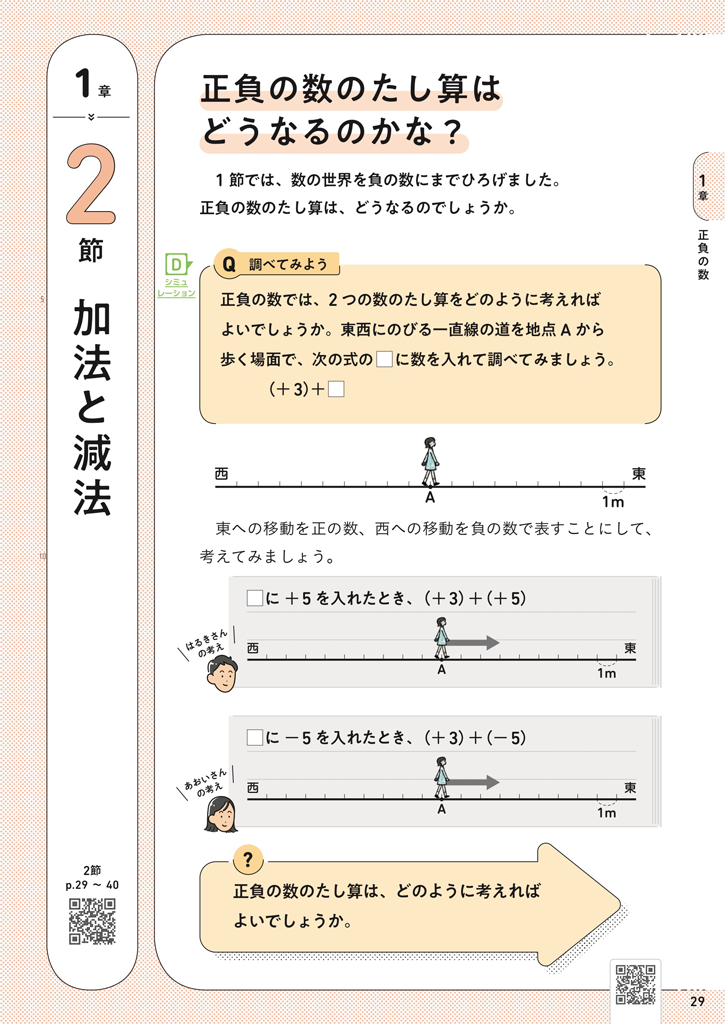
この場面での加法の意味は、（1回目の移動）と（2回目の移動）の結果と考えることができます。矢線図でいえば、1回目の移動の矢線の終点を2回目の移動の矢線の始点とすることであり、和は原点から2回目の矢線の終点までの移動に対応するということですね。
ここでは、□に様々な数を入れ、その加法がどのような移動を表すかを生徒が考えながら、2つの移動の結果として、加法の意味をとらえていきたいところです。

授業で扱う際には、実際に生徒に移動させたり、QRコンテンツを活用したりするなど、実感を伴って理解できるようにくふうしたいところですね。

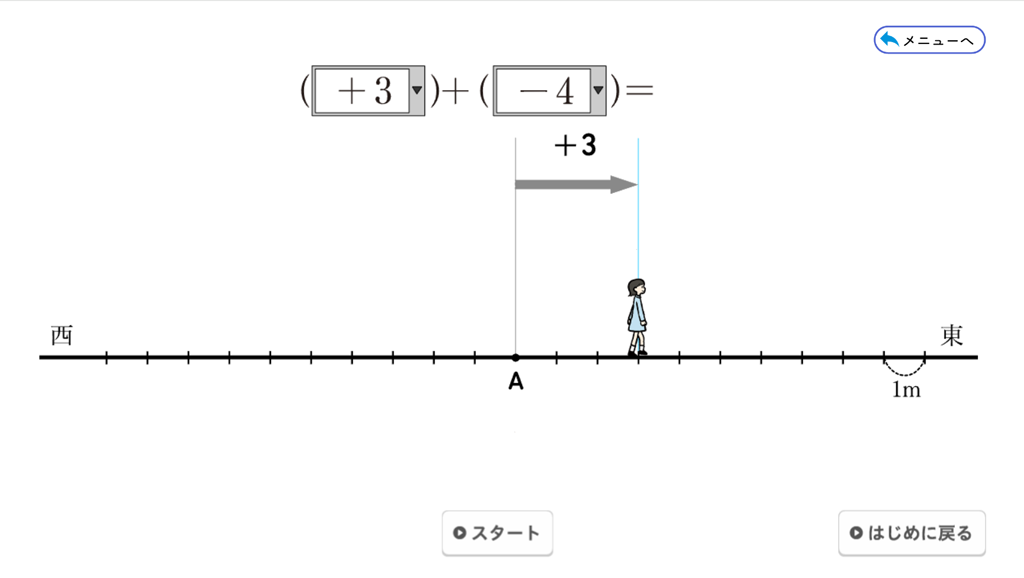
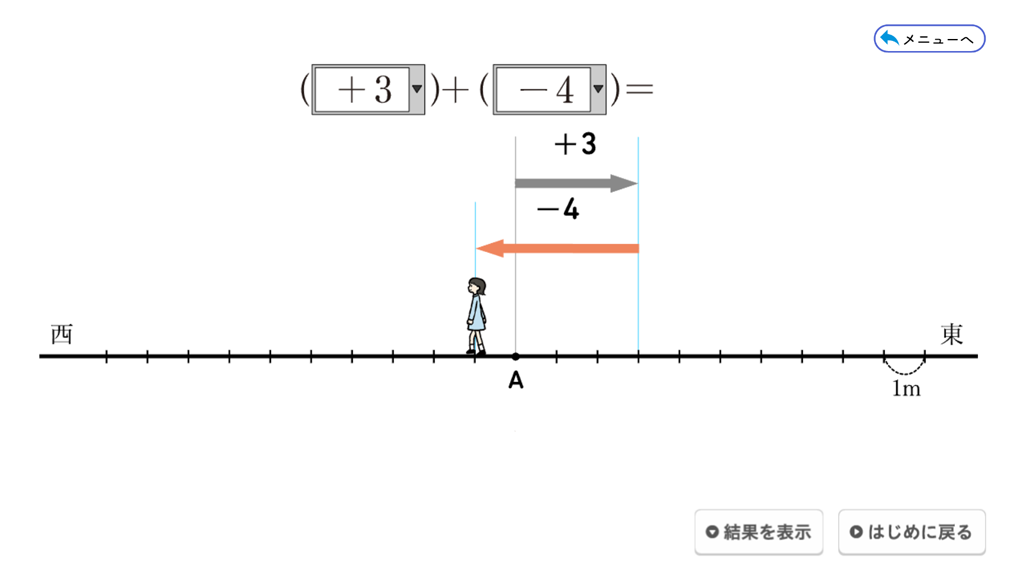
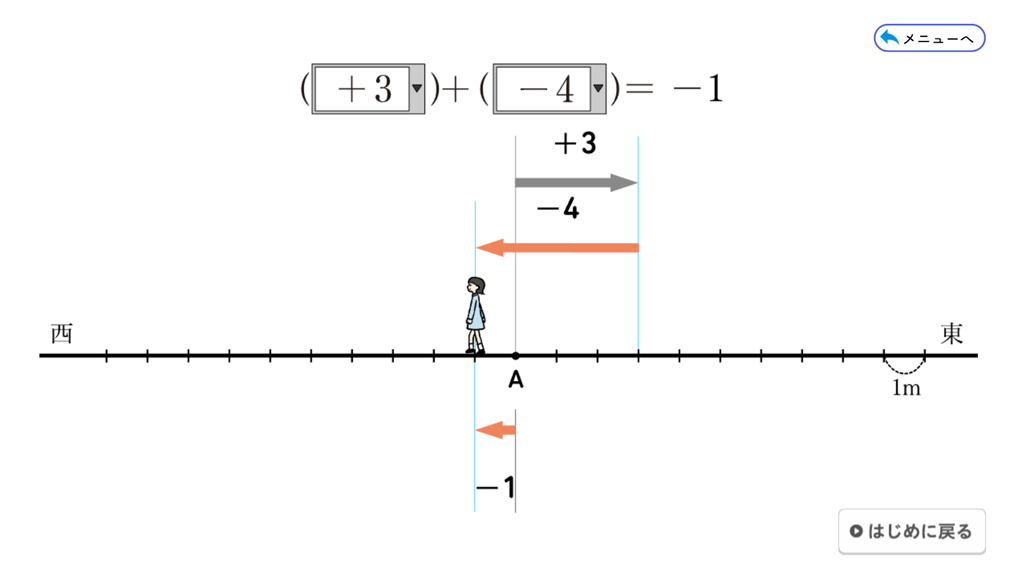
QRコンテンツでは、□に入る数を\(-5\)から\(+5\)までの整数から選択することができ、それぞれについて、移動する様子を見ることができます。 例えば、□に入る数が \(+3\) と \(-4\) のとき、最初に \(+3\) で、東に \(3\) 移動します。次に \(-4\) で、西に \(4\) 移動します。その結果を表示すると結果的に「\(-1\)」移動していることが分かります。QRコンテンツで□に入る数を変えて移動する様子を見ながら、正負の数の加法の意味を理解できるようにしたいですね。

QRコンテンツはこちら

＞東西の移動でたし算を考えよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。