今日の授業のひと工夫（小中学校）
- TOP
- 今日の授業のひと工夫（小中学校）
- 【2年4章】証明のすすめ方②
「新しい数学」2年4章p.119Qは、条件（仮定）にもとづいて図をかき、証明する性質（結論）を自分で見いだしていく、探究的な問題です。
教師がQのように問いかけると、
～
のような性質が生徒から出てくることでしょう。❶のように、そのうちの1つについて証明し、さらに証明を読むことで証明を評価・改善したり、新たな性質を見いだしたりして、証明の理解を様々に深めることがねらいです。
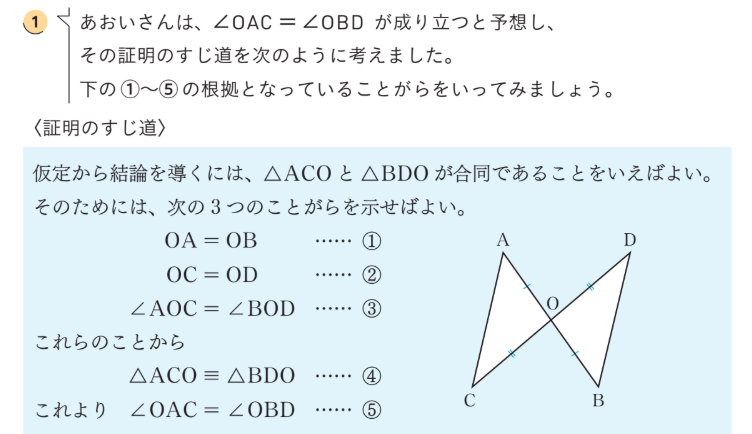
❶では、証明を「書く」ことだけでなく、証明を「読む」ことを大切にしたいところです。証明を読むことで、「△ACO \(\equiv\) △BDO」から「AC = BD」「\(\angle\)OCA = \(\angle\)ODB」と新たな性質を見いだすこともできます。また、結論として証明した「\(\angle\)OAC = \(\angle\)OBD」から、さらにどんなことがいえるかを考えてもよいですね。はじめに予想したAC\(/\!/\)DB（
）や四角形ACBDが平行四辺形であること（）もいえるでしょう。
証明のためにかかれた図が代表であり一般性をもつことを理解するのは、生徒にとって簡単なことではありません。仮定が同じであっても、図が異なったり、図の向きなどが異なったりすることで、証明が異なると考えたり、証明しなおさなければならないと考えたりする生徒がいます。❷の発問をきっかけに、そうたさんの図を使ってあらためて証明をしたうえで、❶の証明と比較し、仮定が同じであれば証明はそのまま変わらないことを確かめることが大切です。
関連記事はこちら
その他のコンテンツ