今日の授業のひと工夫（小中学校）

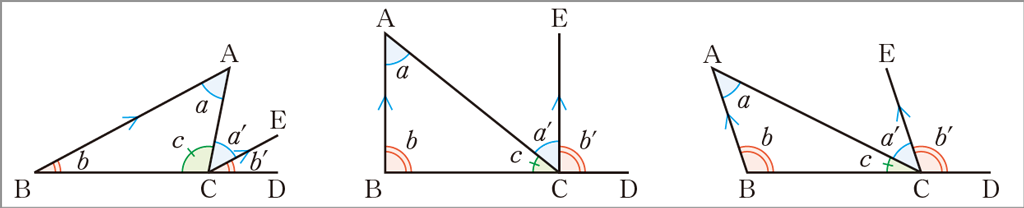
いろいろな位置に平行線をひくことで、三角形の内角の和が180°であることを証明できます。p.105や問8は三角形の頂点に3つの角を集める方法で、このような証明の典型例です。これらを例として他の方法を生徒に考えさせると、集める頂点が違うだけのものも出てくるでしょう。いろいろな方法を発表しながら整理し、次のことに気づいていくようにしたいところです。

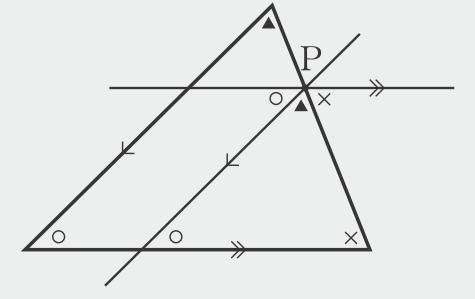
ほかにも、次の三角形のように、平行線をひいて点Ｐのまわりに内角を集めることを考えてもよいですね。

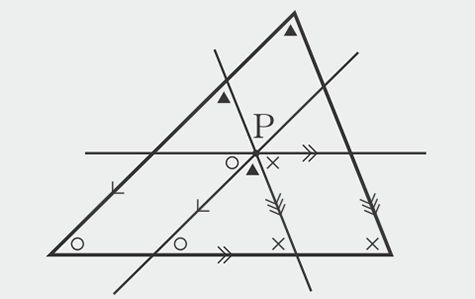
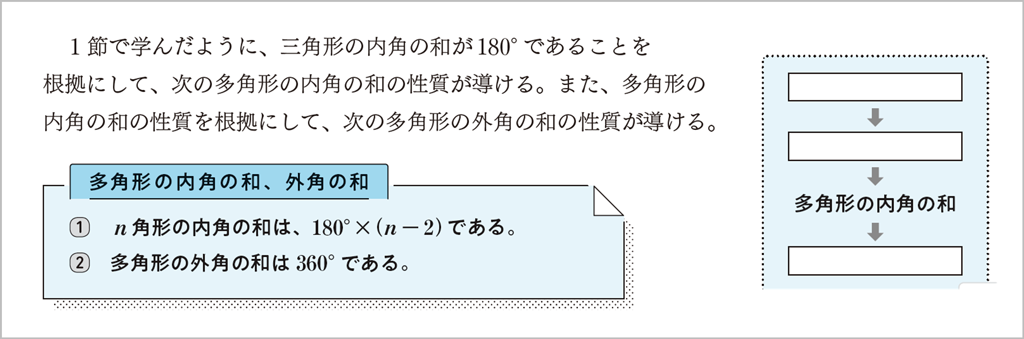
ここでは、三角形の内角の和が 180°であることは平行線の同位角や錯角の性質をもとに証明できたことと、1節で考えてきたことをふり返り、何をもとにして何を導いたかという説明のしくみを整理しています。右の図と対応させて振り返るとよいでしょう。

ここで学んだ考え方や見方は、次ページの「角の大きさを求める方法を考えてみよう」で生かすことができます。大切にしたい見方、考え方なので、多面的に考えることのよさも一緒に丁寧に扱いたいところですね。