今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【1年4章】満水になるまでの時間を予想しよう

「新編 新しい数学」1年4章p.118、119では、水そうが満水になるまでの時間を知りたいという現実場面の問題を、比例の考えを使って予想します。そのことを通して、「自分が捉えようとすることがらを、わかりやすい数量におきかえて考える関数の考え」や、「現実の問題を理想化、単純化して数学の問題におきかえる」という数学的な考えを意識させることが大切です。
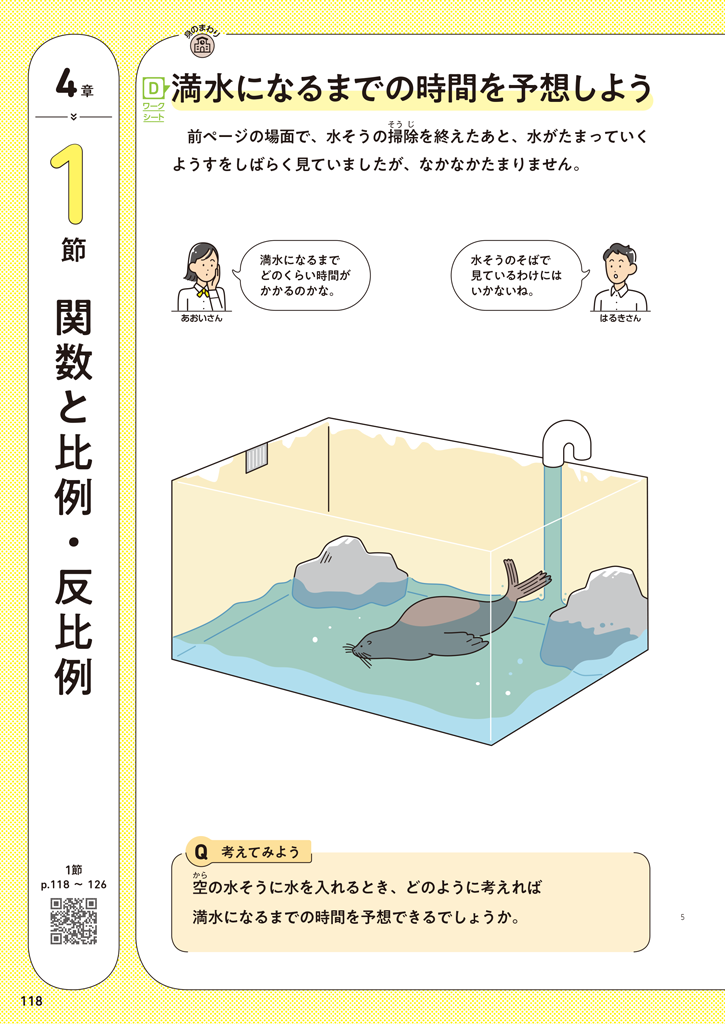
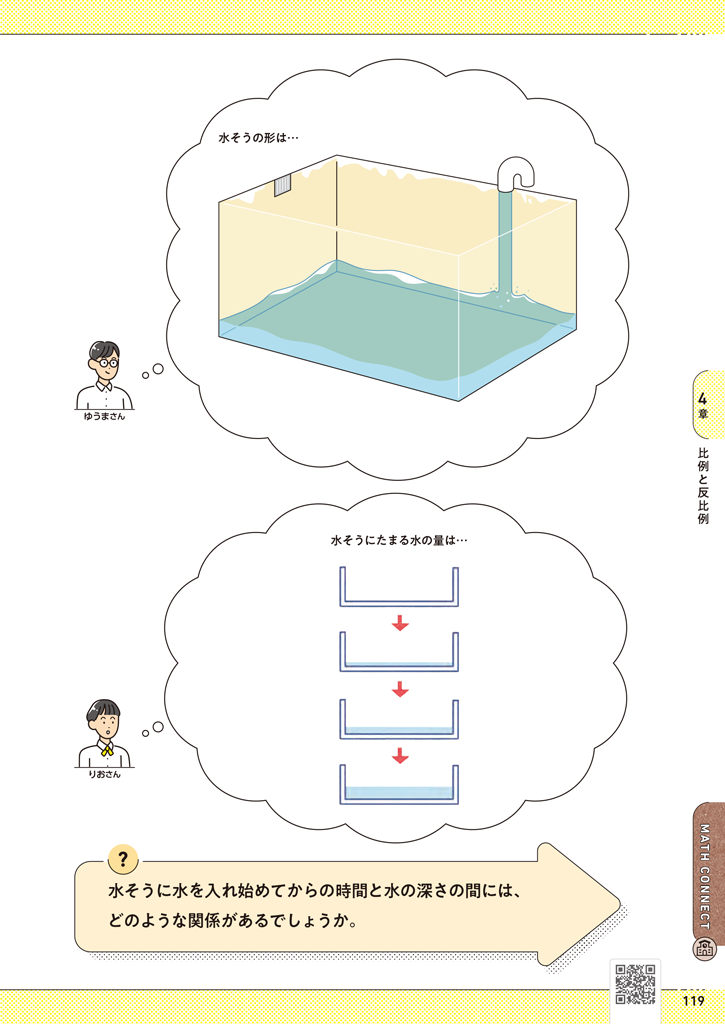
▲1年 p.118、119
Qでは、満水になるまでの時間ではなく、その時間を求める考え方について聞いています。例えば、生徒から予想できないという反応があったら、教師から「なぜ予想できないのか」とその理由を生徒から引き出すことが考えられます。
一方で、予想する方法として生徒から1分間でどのくらい水がたまるかを調べるという方法が出てきたら、実際に何を調べたらよいのかを問いかけることが考えられます。ここでは、問題解決の過程を重視し、それを生徒に意識させたいところです。
ここでは、「満水になるまでの時間を水の深さ(水そうの深さ)におきかえて考える」という関数の考えを引き出し、それを意識化することが主なねらいです。水の深さ以外にも、水そうにたまる水の量(容積)におきかえるという考えも出てくるかもしれませんね。その場合、自分たちが測ることができる量は何かと問い、水の深さに結び付けるとよいでしょう。
また、満水になるまでの時間を予想するために必要な情報を考えることも大切にしたいところです。水の深さや1分間にたまる水の量といった反応が予想できます。例えば、水の深さについては「どこも水の深さは同じなのか」、1分間にたまる水の量については「実際に測ることができるのか」「なぜ1分間のときだけわかればよいのか」など「なぜそれがわかると時間を予想できるのか」を問い、考えさせることで、吹き出しで示しているような仮定を顕在化させることができますね。
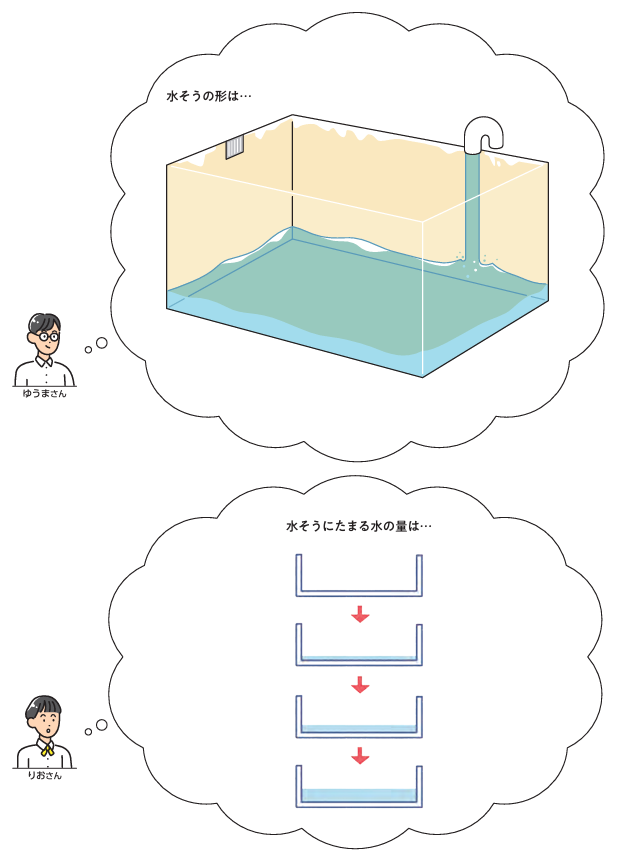
吹き出しでは、現実の問題を、比例の考えを使って解決できるようにするためにおく「仮定」を明らかにすることを意図しています。こうした仮定をおくからこそ、比例の考えを用いて満水になるまでの時間を予想できるようになるということを意識させたいところです。そのためにも、生徒から考えを引き出すような問いかけを大切にしていきたいですね。
その他のコンテンツ
