今日の授業のひと工夫（小中学校）

「新しい数学」3年3章ｐ.89では2次方程式を利用して、動点に関する問題を解いていきます。

動点の問題では、まず場面をうまくつかむことが大切です。例3で、生徒が場面を把握しやすくするために、Dマークコンテンツを使って、実際に点P、Qを動かして\(\triangle\)APQのようすをみることができます。

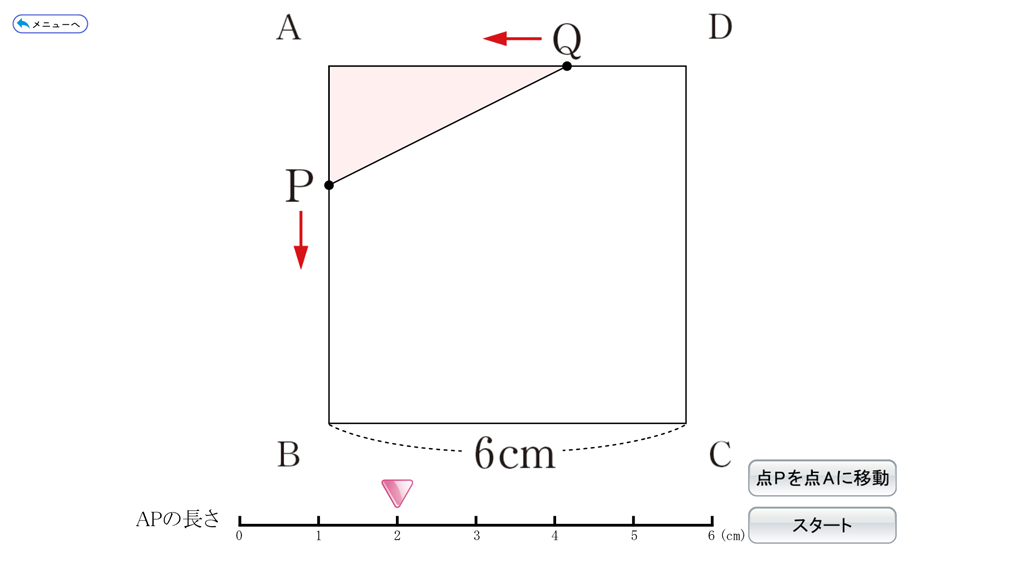
また、点Pが 1cm、2cm、…と動いたときのようすを図にかき\(\triangle\)APQの面積を求めることも場面把握に有効です。このような問題では、すぐに方程式をつくって解を求めることが多いですが、ここでは、点Pの動いた長さと\(\triangle\)APQの面積の表をつくらせる活動を行うなど、関数的な見方も大切にしたいところです。

次章の「関数 \(y=ax^2\)」につながる場面として、表をつくる活動をとりいれることも考えられますね。下の表から\(\triangle\)APQの面積が3cm\(^2\)になるのは、点Pの動いた長さが1cmと2cmの間と、4cmと5cmの間の2回であると予想することができます。

例3の問題では、前章の学習をふり返り、\(\sqrt{3}\) の近似値を確認して、解の吟味を行う必要があります。\(1\lt\sqrt{3}\lt2\) であることから、\(3+\sqrt{3}\) 、\(3-\sqrt{3}\) のどちらも \(x\) の変域である \(0\leqq x\leqq 6\) を満たしていることを確認します。

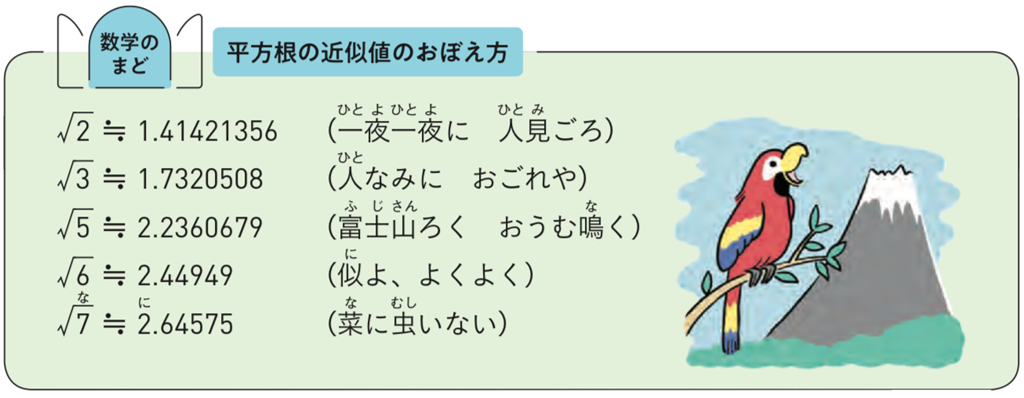
さらに、p.55 の数学のまどにあるように \(\sqrt{3}\fallingdotseq 1.73\) であることを利用して、\(3\pm\sqrt{3}\) の近似値を求めると、\(3+\sqrt{3}\fallingdotseq 4.73\) 、\(3-\sqrt{3}\fallingdotseq 1.27\) となります。これらの値は、1cmと2cmの間と、4cm と5cmの間にあるという予想と合致していることも確認できますね。

QRコンテンツはこちら

＞点が動くようすを見てみよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。