今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【3年3章】解の公式を使って、2次方程式を解いてみ…

「新編 新しい数学」3年3章p.79では、前ページで導いた解の公式を使って、2次方程式を解きます。

解の公式を使って2次方程式の解を求めるには、これまで学んできた数の計算、文字式の計算、平方根の計算の処理ができる必要があります。つまり、解の公式の利用は、まちがいやすい処理を多く含んでいます。そこで、解の公式を学んだ直後でもあるので、まず、公式の基本的な適用を意図して、例1、問1、問2(1)、(2)はできるだけ余分な計算処理要素を含まない型を扱い、問2(3)、(4)では\(\sqrt{a^2 b}=a\sqrt{b}\)の変形のみが含まれるものを扱っています。次ページでは、さらに約分が必要なものを扱い、段階的に学習を進められるようにしています。

問2(3)や(4)では解を \(x=\frac{11\pm \sqrt{125}}{2}\) や \(x=\frac{5\pm \sqrt{45}}{10}\) のように、根号の中の平方因数を根号の外に出さずに解答する生徒がいるかもしれません。次ページからこの考えを多く使うため、ここで確認しておきたいですね。また、(4)ではさらに \(x=\frac{1\pm 3\sqrt{5}}{2}\) や \(x=\frac{1\pm \sqrt{45}}{2}\) のように、 分母の10と5を約分してしまうかもしれません。1年 p.80 例10の学習内容をもう一度確認しておきたいですね。
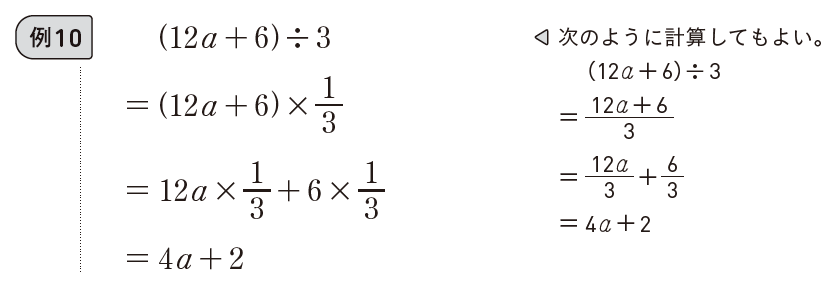
実は、問2(3)、(4)のように\(\sqrt{ }\)の中を簡単にできても約分はできない、\(a\)、\(b\)、\(c\) の値が1桁の整数である2次方程式は非常にまれなものなんです。この型の2次方程式をいくつか例を示すので、これらを類題として取り上げて、是非活用してみてください。
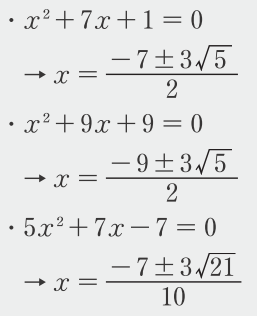
その他のコンテンツ
