今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年2章p.51では、新たに学んだ根号をふくむ式の計算方法を活動を通して理解させます。まずは、乗法について、\(\sqrt{a} \times \sqrt{b}=\sqrt{a \times b}\) が成り立つかどうかを考えましょう。

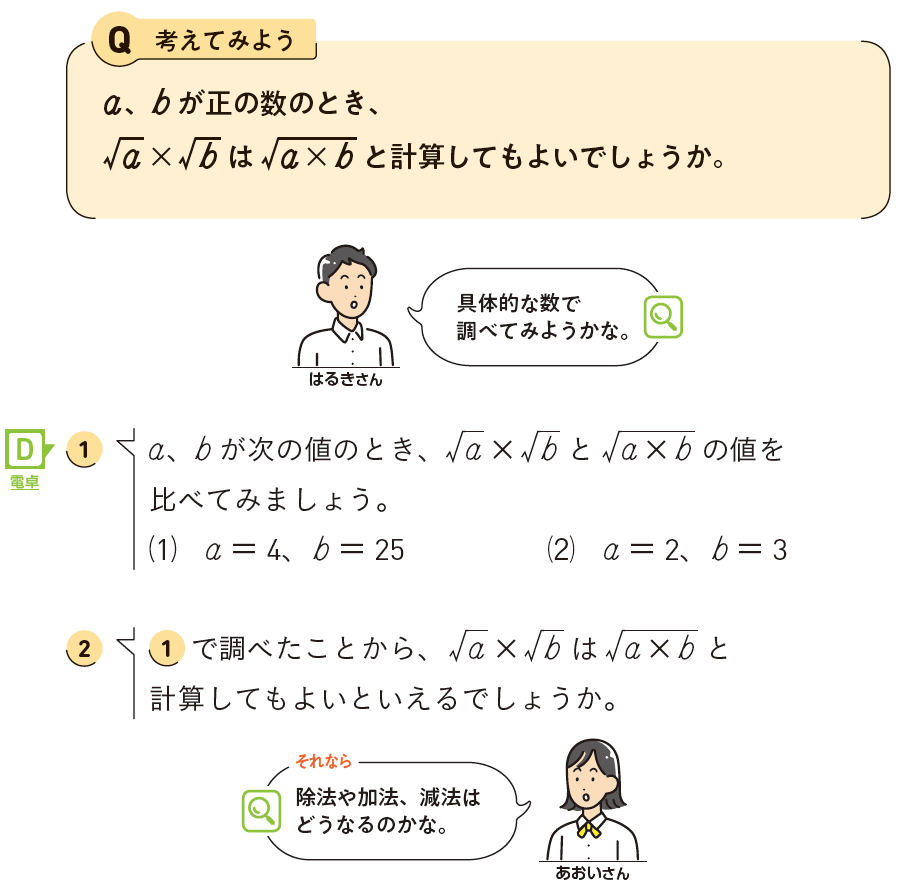
①の活動では、\(\sqrt{a} \times \sqrt{b}\) と \(\sqrt{a \times b}\) が何となく同じであると考えたり、無意識に同じものとみなしたりして、一方だけを計算する可能性があります。計算できる根拠を問いかけたり、計算の過程をきちんと示させたりして、しっかり取り組ませたいですね。

また、①では具体的な数について式が成り立つことを調べて説明しています。これだけでは、いつでも同じように計算できるとはいえないことから、 文字を使って\(\sqrt{a} \times \sqrt{b}\) と \(\sqrt{a \times b}\) が等しいことを説明できないかを考えます。平方根と平方の関係を再確認し、\(\sqrt{a} \times \sqrt{b}\) と \(\sqrt{a \times b}\) のそれぞれを2乗して、同じ数になるか確かめます。

ただし、文字での証明に抵抗感を示す生徒もいるため、\(a=2\)、\(b=3\) とした場合の式と、\(a\) と\(b\) を用いた式とを見比べながら確認することも考えられますね。

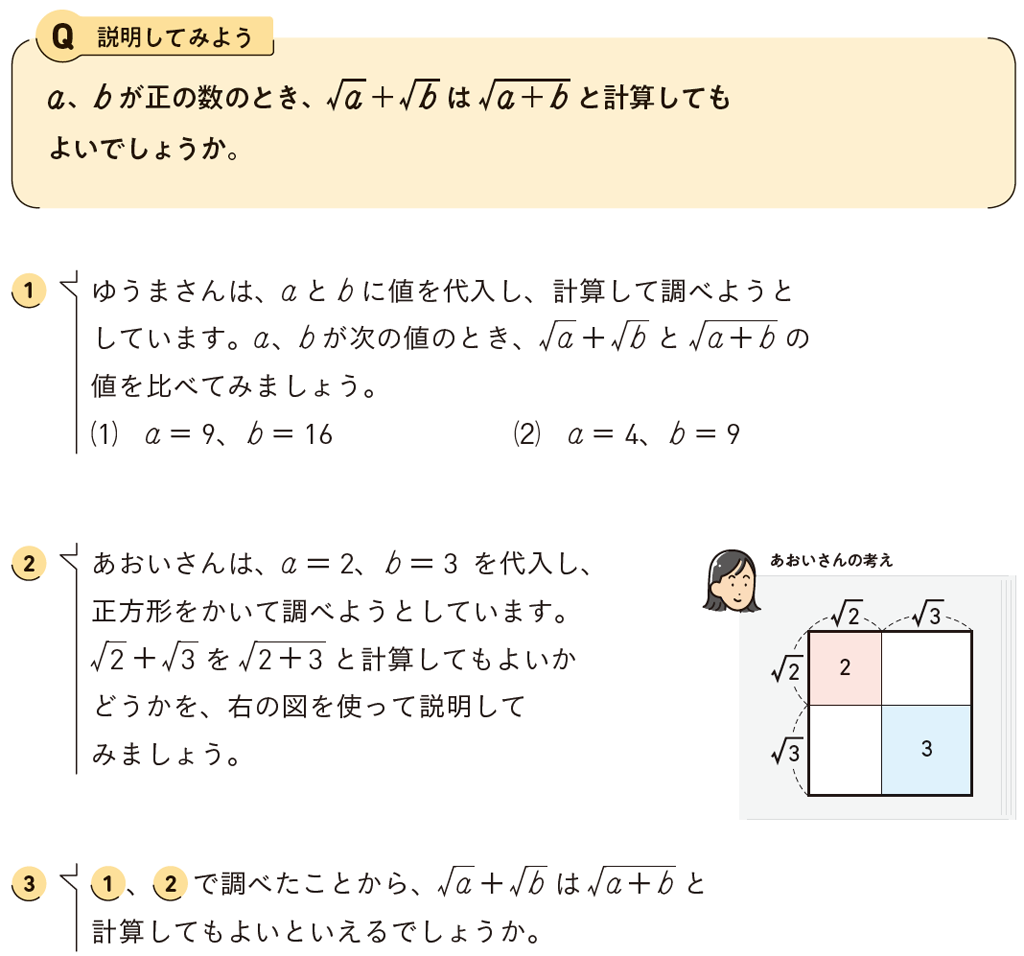
ｐ.57の根号をふくむ式の加法の計算方法も、この乗法と同じように具体的な数について\(\sqrt{a} + \sqrt{b}\) と \(\sqrt{a + b}\) の値を調べ、等しいかどうかを考えていきます。①での活動から、\(\sqrt{a} + \sqrt{b}\) と \(\sqrt{a + b}\)が等しくないことに気づかせ、その理由を説明させます。p.51 の乗法を考える際の経験を生かして、生徒が多様な方法で説明することを期待したいですね。