今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年2章p.42、43は、平方根の学習の導入として、方眼を使ってかいた正方形には、1辺の長さが整数で表せない場合があることを理解させる教材です。いろいろな面積の正方形をかいて、その1辺の長さをはかります。その値を2乗しても面積と等しくならない場合があるということに気づかせ、いままでに学習した以外の数の存在につなげましょう。

いろいろな面積の正方形をかく活動では、次のように、それぞれの図のもっとも小さい正方形の面積の4倍、9倍、16 倍、…となる正方形をかくことができます。

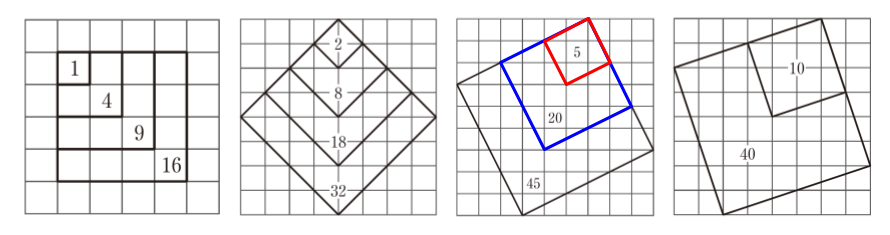
面積が5cm²と20cm²の正方形に着目すると、20cm²の正方形は5cm²の正方形4つ分であり、1辺の長さは5cm²の正方形の2倍になっています。この方法でかいた正方形を1つ取り上げて、1辺の長さや面積の関係について考えさせてもよいですね。

p.58のQでは、この面積が5cm²と20cm²の正方形の関係をもとに、同じ数の平方根をふくむ式の計算方法について考えます。

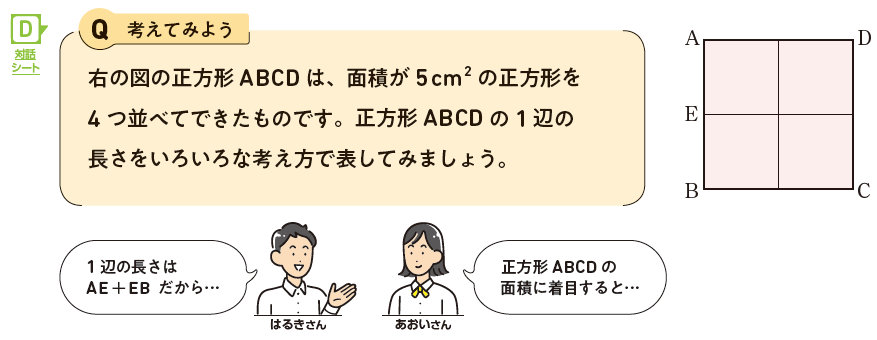
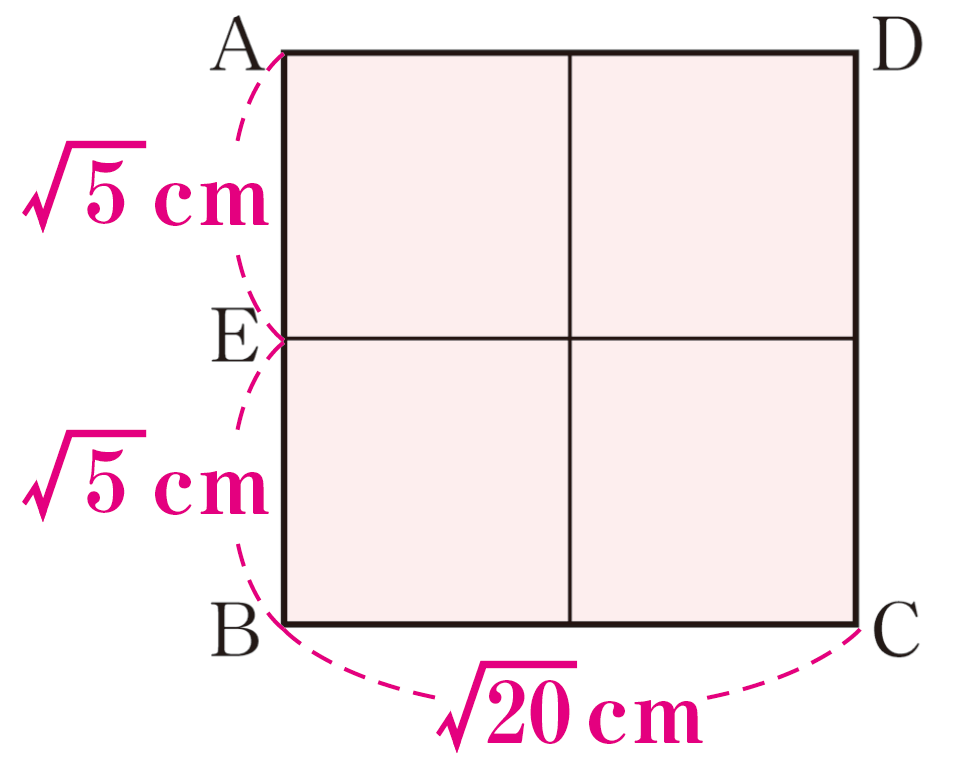
全体の面積で考えると、正方形ABCDの面積は20cm²なので、1辺の長さは \(2\sqrt{5}\) cmとなります。AEとEBは、それぞれ面積5cm²の正方形の1辺の長さなので、AE+EBは \((\sqrt{5}+\sqrt{5})\) cmです。また、導入の活動で見つけたことから、ABは \(\sqrt{5}\) の2倍の長さであることがわかります。これらのことから、\(\sqrt{5}+\sqrt{5}=2\sqrt{5}\) の計算につなげることができます。はるきさんやあおいさんの吹き出しをきっかけに生徒の考えを引き出し、数の性質を図形で考えることのよさを感じさせたいですね。