今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年1章p.33のQは、数の性質を予想して、その性質が成り立つことを式の計算を利用して証明するものです。

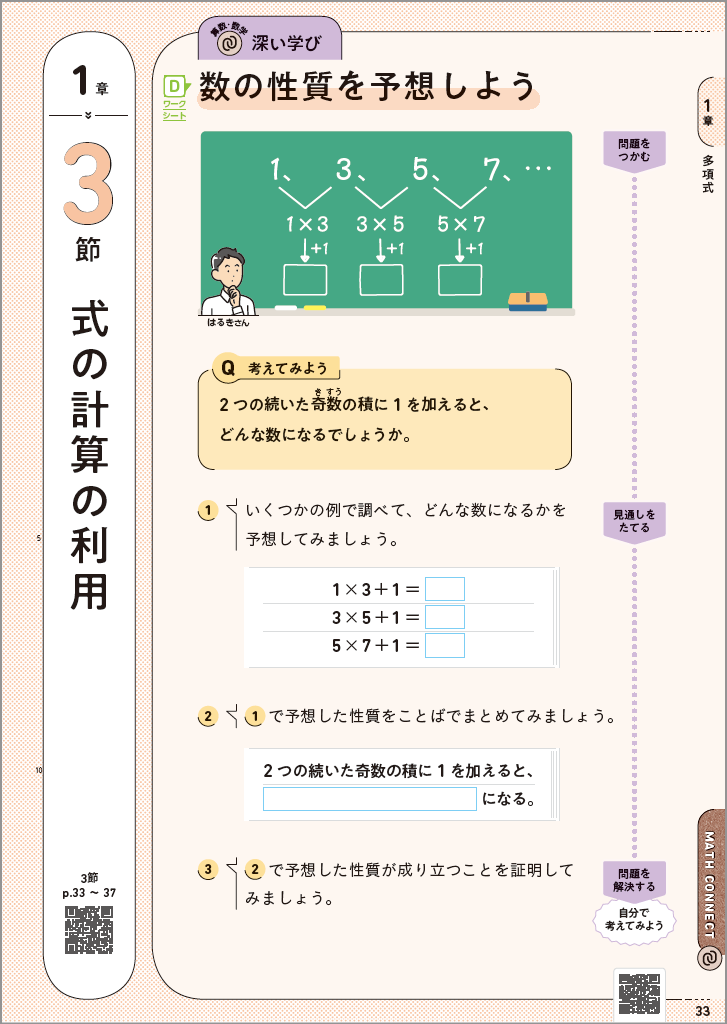
①において、いくつかの例で調べながら成り立つ性質を予想する場面では、生徒からより多くの意見を引き出せるとよいでしょう。②では、これまでの学習と同じように予想を命題の形で表し、証明することがらが明確になるようにしたいですね。ここで出てきた意見は板書しておき、⑤の場面で振り返るとよいでしょう。

続いてp.34では、教科書のようにはるきさんの予想を提示してもよいですが、①で出てきた学級の生徒の意見を取り上げて共有したいですね。まずは、自力解決する時間をとり、発表する形でクラスで共有してもよいでしょう。
証明部分の文字を用いた説明の手順は、2年で一度学習していますが、生徒の実態に応じてあらかじめ示したり、共有した証明を振り返りながら、あらためてまとめたりすることが考えられます。

⑤は計算結果をどう変形すれば、「ある数の2乗になる」ことを証明することができるのかを考える場面です。①で「平方数になる」「ある数の2乗になる」と予想した生徒がいれば、「この証明を見て気づくことがないか」と問いかけて、この証明の式を少し変形することで、予想した命題が証明できることに気づかせるとよいでしょう。

教科書の証明では、\(4n^2+8n+4=(2n+2)^2\)と変形すると、「ある数」が見えるようになることに気づかせます。式が表す数量を、証明のなかで読み取ることで、式を読む力の向上につなげていきたいですね。

関連記事はこちら

＞【2年1章】式による証明