今日の授業のひと工夫（小中学校）

1年1章3節では、乗法の負の数への拡張を2つの方法で考えます。まずp.39で九九表をもとにした拡張を行い、次にp.40で具体的な場面として速さを題材にして負の数の乗法を考えていきます。このように2通りの方法で考え、同じ結果が得られるかを調べることは、数学に限らず重要な考え方です。このことも、ここでの学習を通して生徒に伝えたいですね。

さて、今回は、p.39の九九表をもとにした拡張について考えていきます。

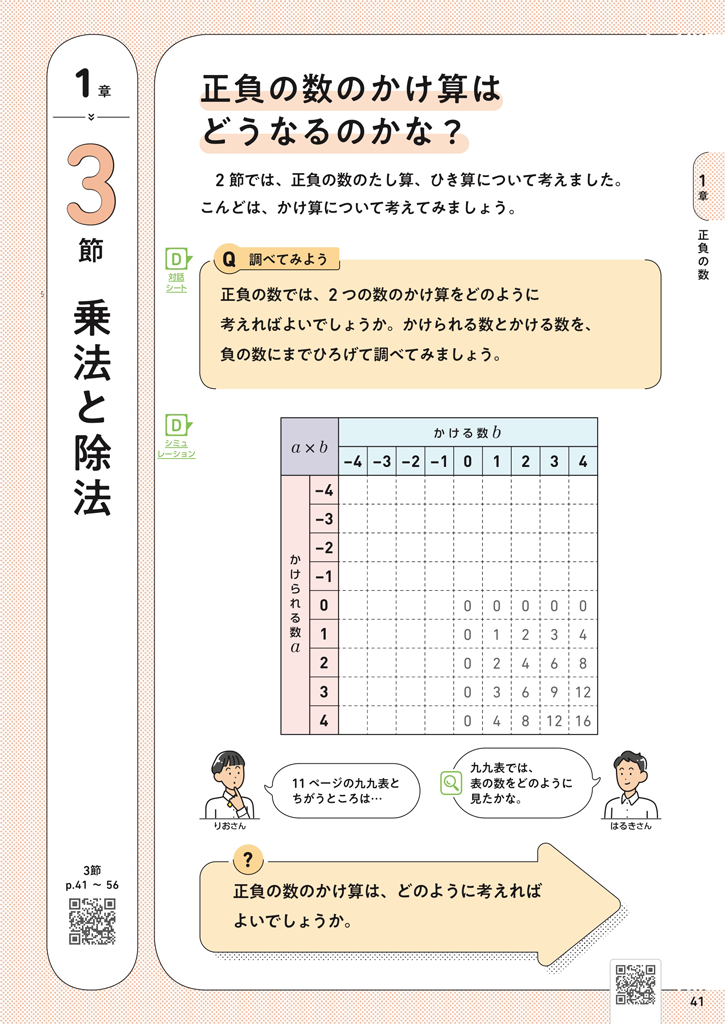
このQでは次のような展開が考えられます。

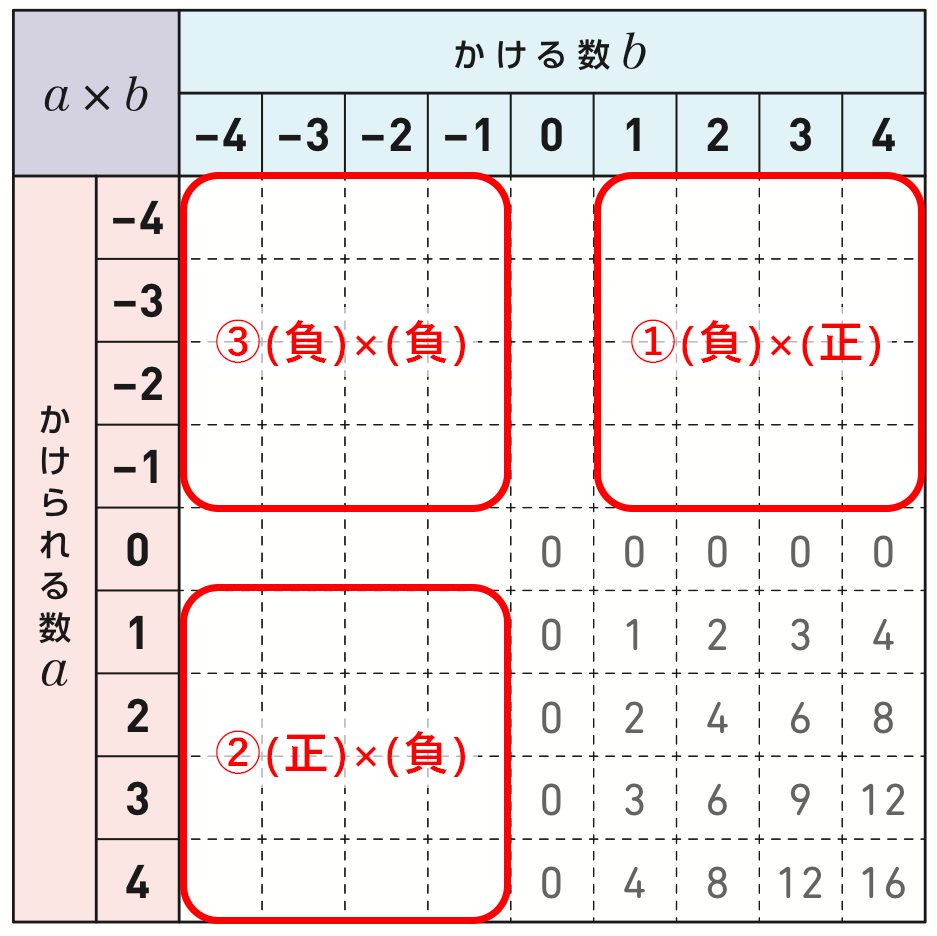
① (負)×(正)
最初に、九九表の右上の(負)×(正)の欄を考えます。各欄に入る数を確認したあとの全体の議論では、例えば\((-2)×(+3)\)を取り上げ、その答えがなぜ\(−6\)になるのかを問います。「\(−2\)が\(3\)つ分だから\((-2)+(-2)+(-2)\)」といった乗法の累加の意味や既習の加法を使った考えが出るでしょう。また、「かける数が\(3\)の列を縦にみていくと\(3\)ずつ減るから\(0\)の上は\(−3\)、その上は\(−6\)」といった正の数の範囲でのきまりを負の数の範囲にひろげて適用する考えも出るでしょう。

② (正)×(負)
次に、左下の(正)×(負)の欄を考えます。右上の(負)×(正)と同様に各欄に入る数を確認したあと、例えば\((+2)×(-3)\)が\(−6\)になる理由を問います。すると、先の加法の考えでは、「\(+2\)が\((-3)\)個分」となり、説明が難しくなります。そこで、九九表のきまりを使った考えが重要になります。かけられる数が\(2\)の行を左に\(1\)つずつ進むと、積が\(2\)ずつ減るので、\(0\)の左は\(-2\)になり、\(-4\)、\(-6\)と続くことが予想できます。

③ (負)×(負)
さらに、左上の(負)×(負)も同様に、九九表のきまりを使えば、\((-2)×(-3)\)が\(+6\)になると考えることができます。(負)×(負)=(正)になることは、具体的な場面では説明しにくいですが、このように九九表のきまりが負の数でも成り立つようにひろげようとすると、(負)×(負)=(正)にならざるを得ないことがわかります。

最後に、九九表全体を振り返り、「左上と右下(同符号どうしのかけ算)は正の数、右上と左下(異符号どうしのかけ算)が負の数」「絶対値が等しい数は、\(0\)を境にして対称に並んでいる」などに気づかせたうえで、次の活動につなげたいところです。