今日の授業のひと工夫（小中学校）

「新編 新しい数学」2年p.34 章の問題B \(\boxed{\ 7\ }\) では、カレンダーの数の並びにかくれた性質について考えます。

(1)では、「縦に並んだ3つの数の和がいつでも3の倍数になること」を説明します。

(2)では、予想が正しくないことを説明します。ことがらが成り立たないことを示すには、反例を1つあげればよいことを指導したいですね。

一方で、下のように8でくくって説明しようとする生徒もいると考えられます。

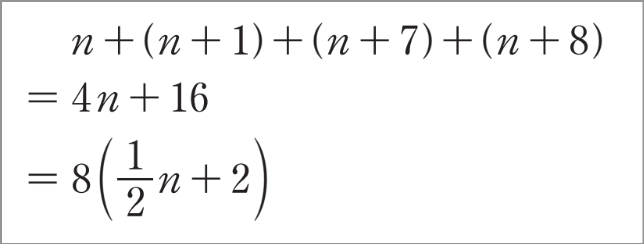
この場合、\(n\) は整数なので「いつでも」整数になるとは限らないことに気づかせたいところです。
なお、\(n\) が偶数の場合、正方形に囲んだ4つの数の和は8の倍数となりますが、式の読み取りとして「4つの数の和が8の倍数になるのは、どのように囲んだときか」と生徒に投げかけてもよいですね。

QRコンテンツでは、カレンダー上で好きな数を選択して囲むと、その和が表示されます。レポート課題として、縦3つや \(2\times 2\) の正方形のほかに、十字や \(3\times 3\) の正方形など、囲み方を変えて考えさせてみるのも面白いですね。

QRコンテンツはこちら

＞囲んだ数の和の性質を予想しよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。