今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【1年1章】正負の数の減法

「新しい数学」1年p.34では、正負の数の減法の意味を理解すること、正負の数の減法を加法になおして計算できることを目的としています。
小学校では、例えば、\(□+3=5\) の \(□\) にあてはまる数は \(□=5-3\) の計算で求めることができることから、減法が加法の逆算であることを学習しました。
p.34のQのねらいは、この「 \(□+a=b\) ならば \(□=b-a\) 」という減法の意味を負の数にまでひろげ、加法をもとに正負の数の減法を考えていくための見通しをもたせることにあります。
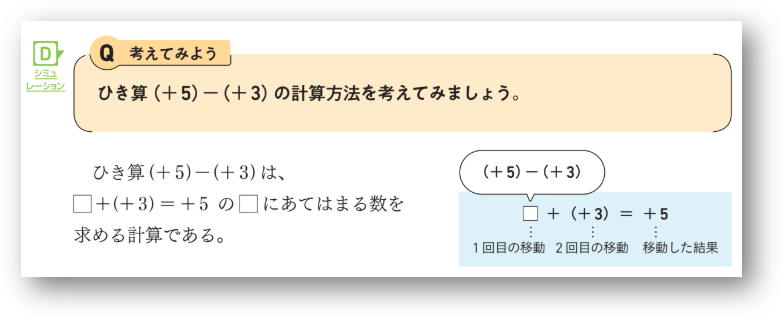
指導では、\((+5)-(+3)\) を \(□+(+3)=+5\) の \(□\) にあてはまる数を求める計算と捉え、加法と同様に東西の移動をもとに考えていくことを確認します。
\(□\) にあてはまる数を、矢線図を使いながら考えていきますが、生徒がこの加法の矢線図を自分でかくことは難しいと思われます。なぜなら、1回目の移動を表す矢印をかこうとすると、終点がわからず作業を進めることができないからです。
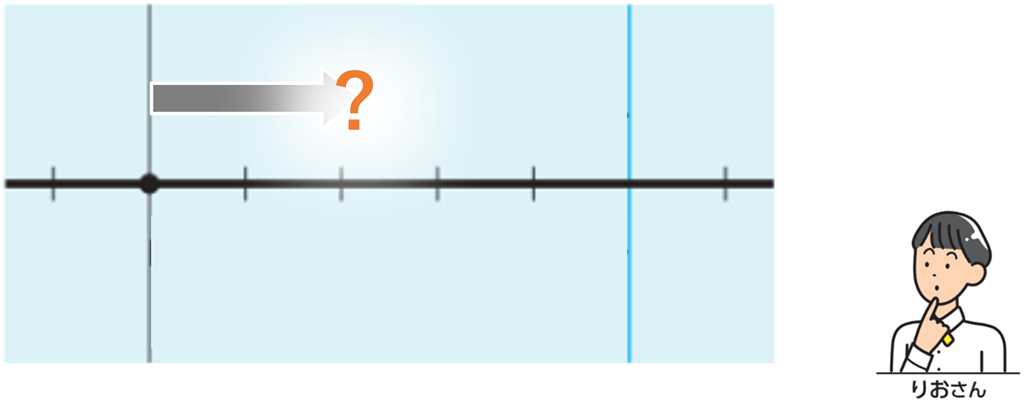
そこで逆に考えて、移動した結果 \(+5\) から \(□\) を考えてみます。まず①で、図㋐のように移動した結果 \(+5\) を表す矢印をもとに、2回目の移動 \(+3\) を表す矢印をかきます。
次に②で、1回目の移動を表す矢印をかくことで、\(□\) にあてはまる数が \(+2\) であると求めさせています。
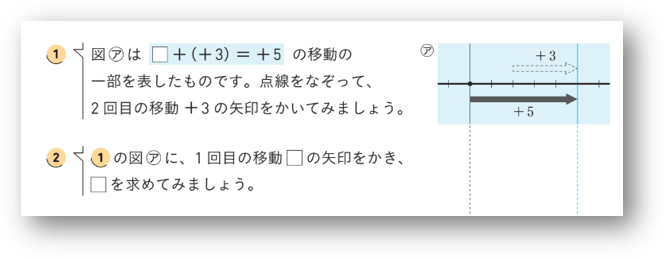
つまり、結果の矢印 \(+5\) の終点が2回目の移動 \(+3\) の矢印の終点と一致することから、2回目の移動の矢印を終点から逆方向に同じ長さだけ伸ばすことで始点が決まります。これにより1回目の移動の矢印の終点が決まるので、その矢印をかくことができます。
このことが、図㋑の考え方につながります。
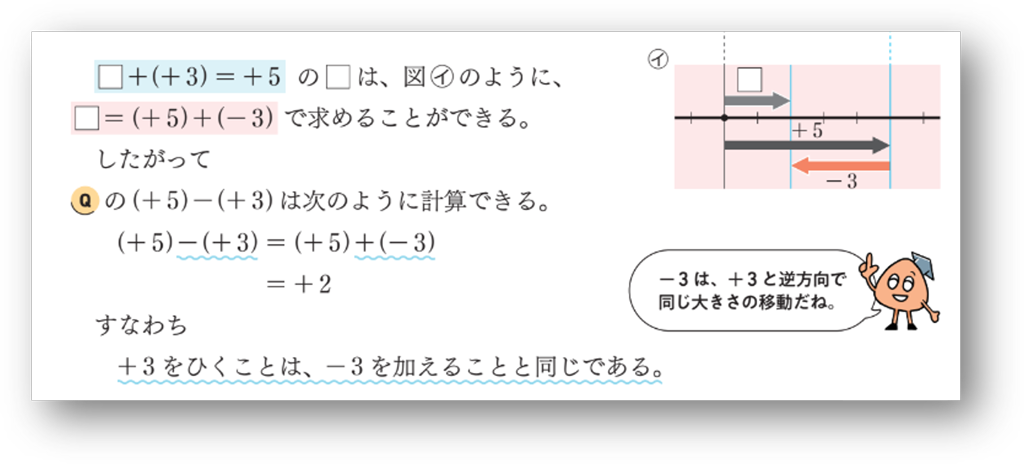
この減法の計算方法については、生徒が発見的に見いだすことが難しいため、先生主導で考えさせたほうが、生徒の混乱は少ないでしょう。しかし、先生が一方的に説明するのではなく、矢線図を使いながら生徒に問いかけ、確認していくことが大切です。
その他のコンテンツ
