今日の授業のひと工夫（小中学校）

「新編 新しい数学」2年1章2節では、数の性質が成り立つことについて、文字を使って説明します。

文字を導入する際には、「数ではすべてを調べつくすことができないので、いつでも成り立つことを説明するにはどうすればいいか」という問題意識を共有したいところです。

授業では、生徒が文字の必要性を実感できることが重要です。例えば、「数をまとめて表すのに何を使ってきたかな」と問い、文字を想起させたり、「なぜ文字を使うのか」と問い、文字を使う意味を考えさせたりするとよいでしょう。

p.24からは、節の導入で見いだした予想を証明する方法について考えます。

p.25の③では、証明で用いた式「\(3(n+1)\)」にもう一度着目します。

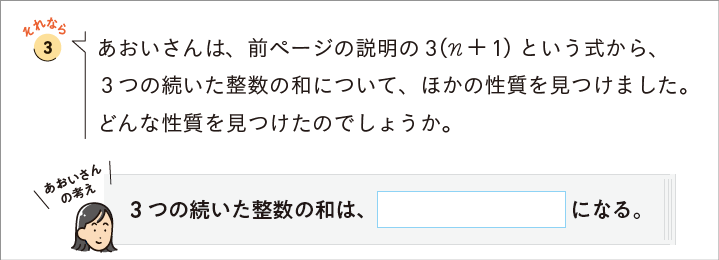
この問いは、変形した式を読むことで、新たな発見ができることを経験させ、式を読む態度を育むことがねらいです。式を読んで「真ん中の数の3倍」という性質を見いだしたら、\(4+5+6=15=5\times 3\) と表し、具体的な数で確認することが重要です。

同様に、3年1章の多項式でも「2つの続いた奇数で、大きい数の平方から小さい数の平方をひいた差は、8の倍数になること」を証明したあとに、「4の倍数になる」「偶数になる」といった性質を見いだすことに取り組みます。

上の証明にある \(8n\) は、\(2\{(2n-1)+(2n+1)\}\) と変形すると「2つの続いた奇数の和の2倍」と読むこともできます。

式が表す数量を証明のなかで読み取ることで、式を読む力の向上につなげていきたいですね。

関連記事はこちら

＞【3年1章】式の計算