今日の授業のひと工夫（小中学校）

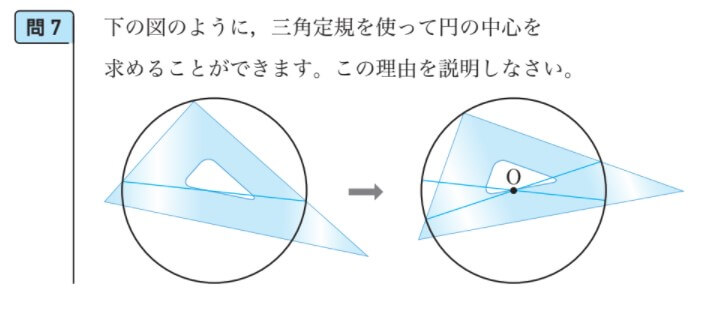
3年6章p.173の問7では、三角定規を使って円の中心を求めることができる理由を説明する問題を扱っています。
次の図において、三角定規の直角の頂点や直角をはさむ2辺と円との交点を、自分で文字をおきながら、図に示された操作を順序立てて説明することを通して、教科書に書かれている
「円周上の3点A、P、Bについて∠APB=90°ならば、線分ABは直径になる。」
ことについて、生徒の理解を深めていきます。

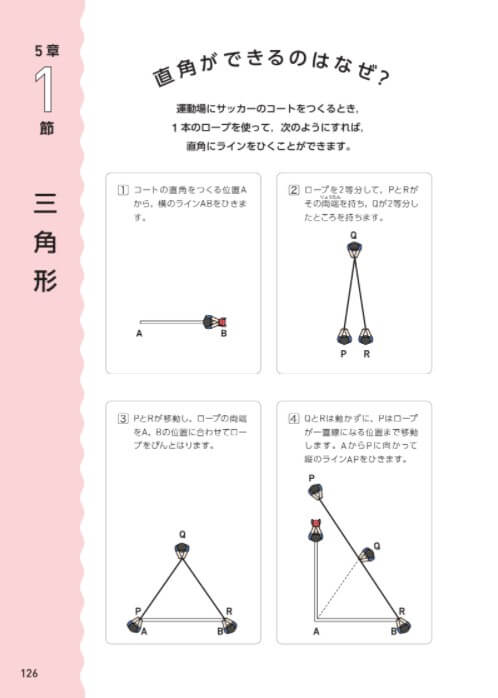
また、図形の性質の理解をより深めるために、2年5章のp.126～127の章の導入を振り返ってみてもよいでしょう。
2年5章の章の導入では、「1本のロープを使って運動場に直角のラインをひく」という場面を設定して、「直角ができるのはなぜ？」を考えていきます。2年では、二等辺三角形を利用して直角をつくる方法に気づかせ、その方法で直角ができる理由を考えさせます。上の問7を学習した後でこれを振り返ってみると、ロープを使った活動は「中心が点Qで、点A、Bを通る円をかいたとき、線分BPが直径となるように点Pをとると∠PABが直径に対する円周角になる」とみることができます。
このように、既習の内容を振り返りながら、図形の性質を深めてみてはいかがでしょうか。

関連記事はこちら
＞ 【2年5章】二等辺三角形の作図