教科書・教材のひと工夫（高校）

　編集委員の先生方に，2025年を中心に大学入試問題で気になった問題と，あわせて取り組みたい『ニューグローバルマーチ数学Ⅰ＋A＋Ⅱ＋B＋Ｃ』の問題を挙げていただきました。
　入試問題の“設定の変化”に対応するには，基本をしっかり押さえることが大切です。

共通解

【編集委員のコメント】

　明治大学では共通解に関する問題が出題されましたが，設定に変化がつけてあります。\(f(x)g(x)=0\) を展開すると5次方程式が出てきてしまいますが，条件を「\(f(x)=0\)かつ\(g(x)=1\)」または「\(f(x)=1\)かつ\(g(x)=0\)」と読み替えることができれば，既知の問題に帰着できます。
　グローバルマーチの問題26のような標準的な問題で，共通解に対する理解をきちんと深めておくことで，変化にも冷静に対応できるでしょう。

２次方程式の解の配置

【編集委員のコメント】

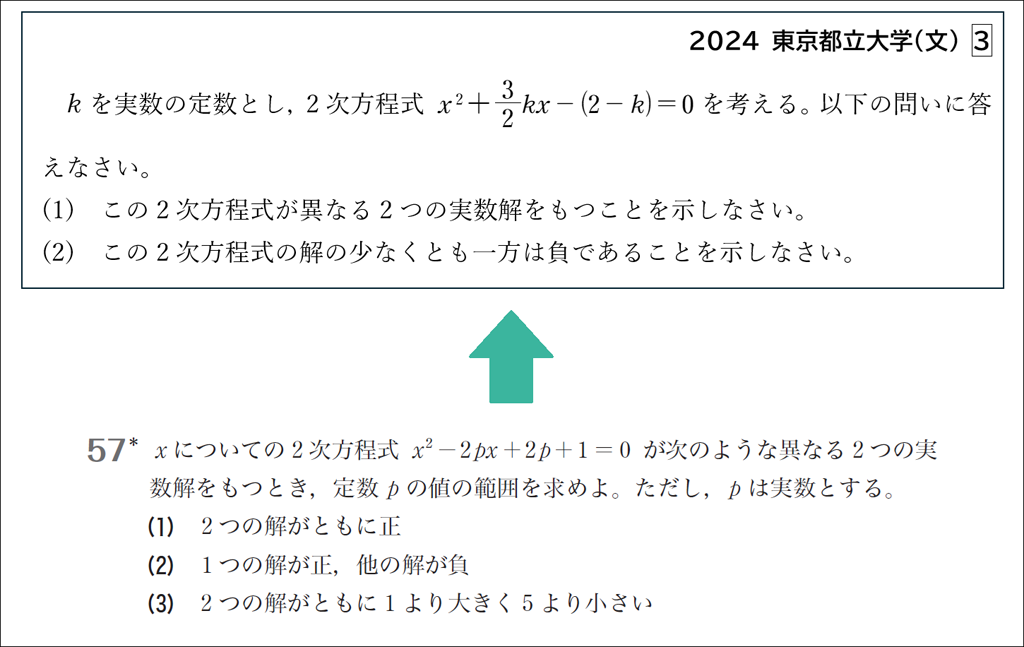
　グローバルマーチの問題57を確実に理解することは大切です。まずは一般的な解法を押さえたうえで，余力があれば放物線 \(y=x^2+1\) と直線 \(y=2p(x-1)\) の関係に着目した考え方も紹介しておきたいところです。
　東京都立大学の問題も，放物線 \(y=x^2-2\) と直線 \(y=-\frac{3}{2}k(x+\frac{2}{3})\) の共有点の \(x\) 座標に注目すれば，\(k\) の値に関係なく小問(1)，(2)ともに成立することが容易に確認できます。

隣接３項間漸化式

【編集委員のコメント】

　グローバルマーチの問題393で隣接３項間漸化式の解法を確認しましょう。しっかりと解法が理解できていれば，岡山県立大学の問題のように \(\{S_n\}\) に関する隣接３項間漸化式が与えられても驚くことはありません。誘導の通りに \(S_n\) を求め，\(a_n=S_n-S_{n-1}(n\geqq 2)\) より \(a_n\) を求めるだけです。最後に \(n=1\) のときを確認することも復習できます。
　時間に余裕があれば，\(\{a_n\}\) がどのような漸化式を満たすかを生徒と議論するのも面白いでしょう。

四面体の外接球の中心

【編集委員のコメント】

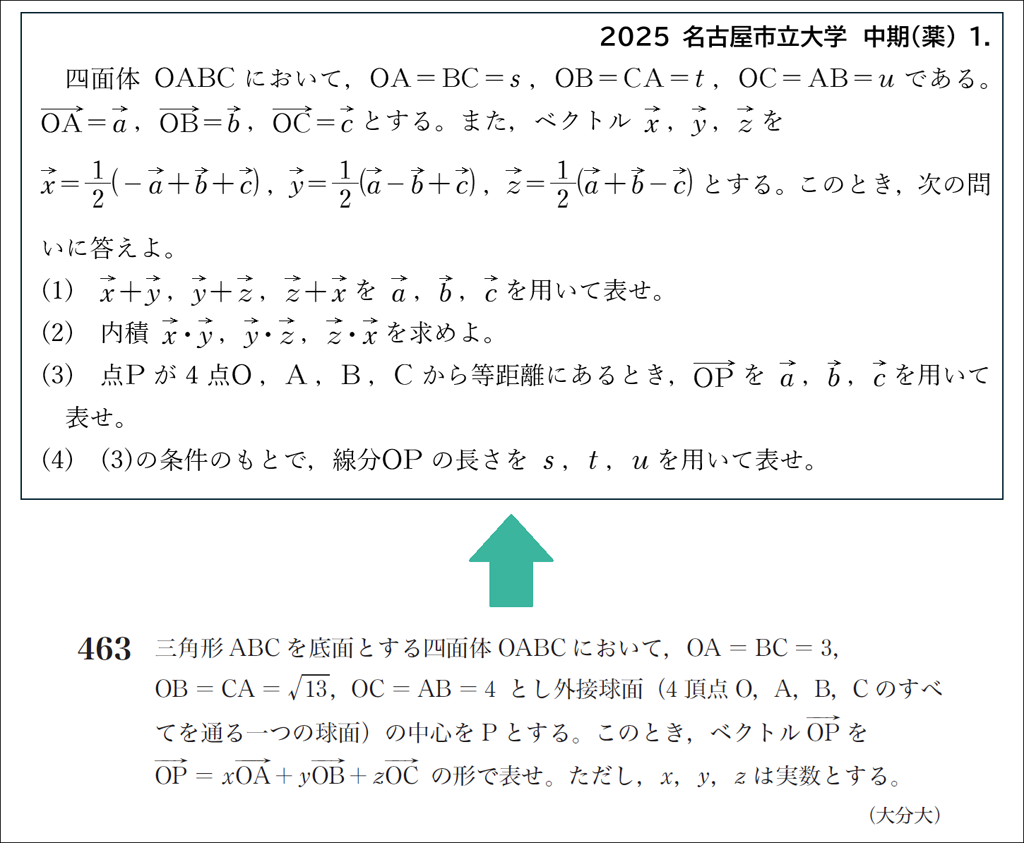
　昔からいろいろな大学で手を替え品を替え出題されている問題です。まずはグローバルマーチの問題463でオーソドックスな解法を確認しましょう。ただし，計算はなかなか大変です。
　等面四面体の性質を利用すれば，あまり苦労せずに求めることもできます。名古屋市立大学の問題では，まさに\(\vec{ x }\)，\(\vec{ y }\)，\(\vec{ z }\) で作られる直方体を利用して考えるように誘導されています。

１のｎ乗根の利用

【編集委員のコメント】

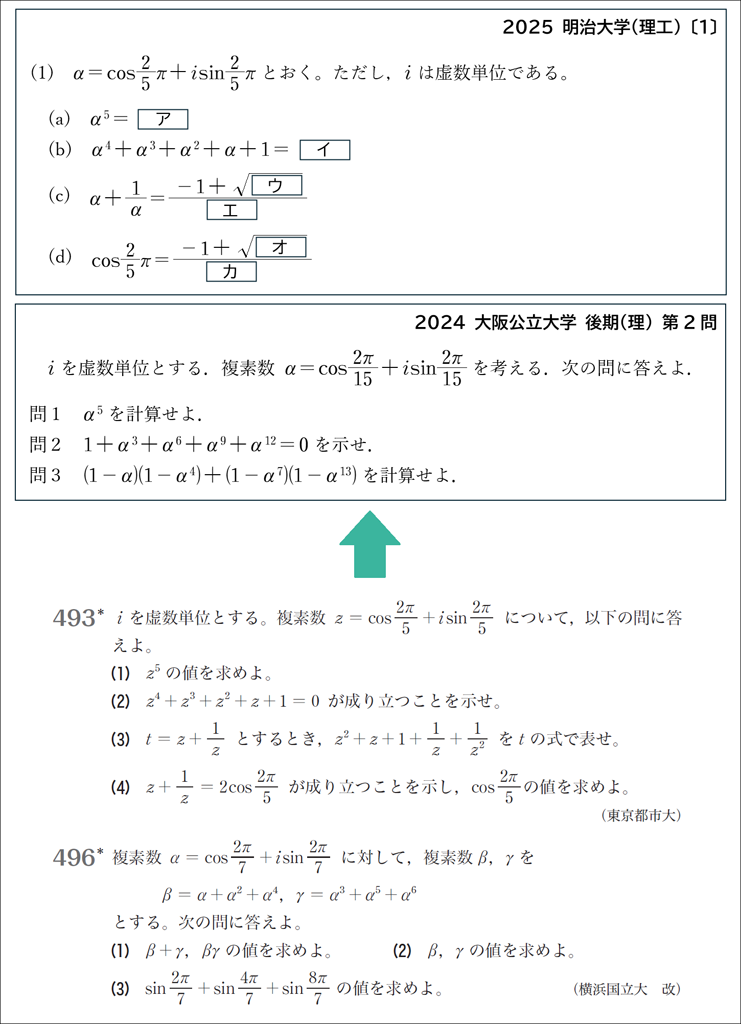
　明治大学の問題はグローバルマーチの問題493と同じ設定です。同年の立教大学（理）でも出題があり，押さえておきたい典型の問題と言えます。
　大阪公立大学の問題は設定に変化を加えていて，小問(2)では \(\alpha ^3\) すなわち１の５乗根をテーマに，(3)では \(\alpha ^5\) すなわち１の３乗根をテーマにしています。やはり設定に変化を加えたグローバルマーチの問題496などを通して，１の \(n\) 乗根について理解を深めておくとよいでしょう。

※入試対策問題集『ニューグローバルマーチ数学Ⅰ＋Ａ＋Ⅱ＋Ｂ＋Ｃ』の詳細は，こちらをご覧ください。