教科書・教材のひと工夫（高校）

　編集委員の先生方に，2025年を中心に大学入試問題で気になった問題と，あわせて取り組みたい『ニューグローバルトップ数学Ⅰ＋A＋Ⅱ＋B＋Ｃ』の問題を挙げていただきました。
　第1回のテーマは，「気づきやアイデアが必要な問題」です。

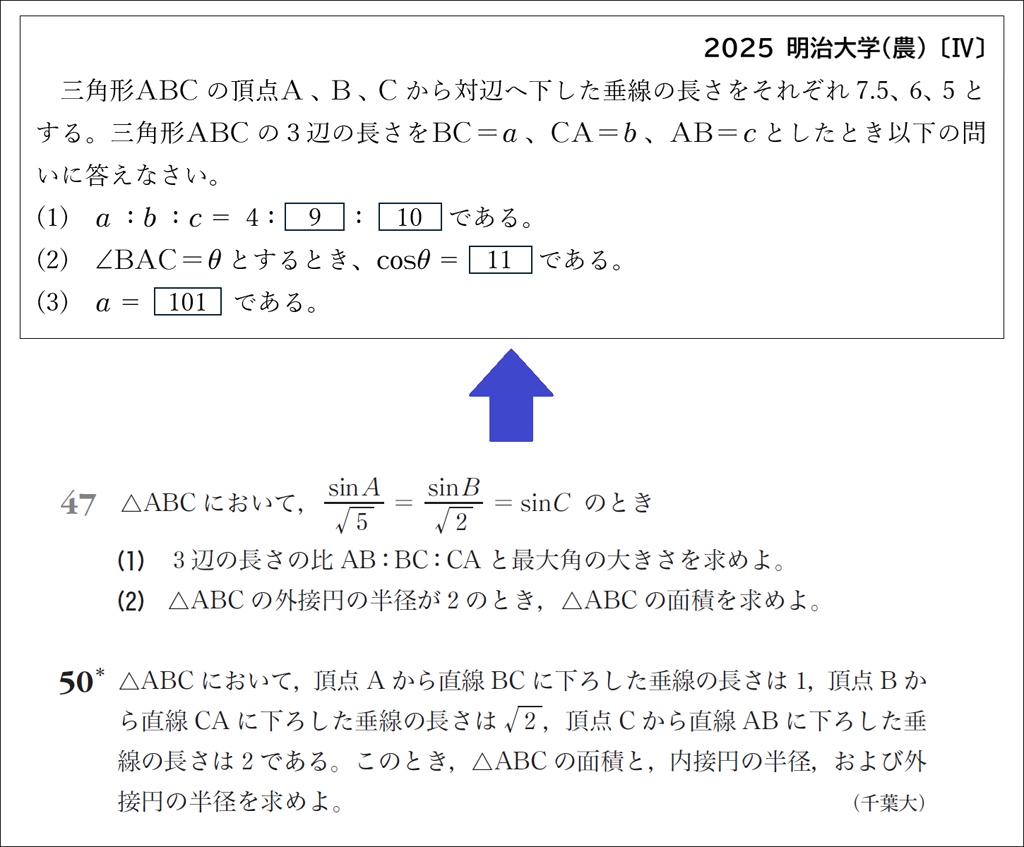
面積の利用

【編集委員のコメント】

　与えられた条件から面積の利用に気づけばよいですが，初見では気づけないまま迷走することもあります。経験があるとないとでは変化への対応力に差が出やすく，是非とも経験しておきたい問題です。明治大学の出題は，誘導が適切で取り組みやすいでしょう。
　グローバルトップの問題47で基本の確認をしたのち，少し変化のある問題50に挑戦したいですね。

完全順列と漸化式

【編集委員のコメント】

　完全順列の総数については，早稲田大学の問題(2)のように漸化式を立てて考えることが重要ですが，誘導がなければこのアイデアに思い至るのは難しいでしょう。まずは具体例を考えることで，漸化式の構造を見抜きやすくなります。
　グローバルトップの問題100をきっかけに，\(n\) 人のプレゼント交換について検討することが期待されます。

２次方程式の解の利用

【編集委員のコメント】

　定番の問題ですが，和歌山県立医科大学の問題は漸化式を軸にしているのに対し，グローバルトップの問題219は \(\alpha^3\text{＝}-1\)，\(\beta^3\text{＝}-1\) を利用した次数下げを軸にしており，アイデアの違いが学べます。グローバルトップの問題411は漸化式を用いて考える問題なので，問題219とセットで取り組むと面白さが増すでしょう。
　また，2025年の新潟大学にも類問の出題があり，見比べると面白いです。

直方体の体積の最大・最小

【編集部のコメント】

　愛知大学の問題は，恐らく文字消去を駆使する解答が想定されているかと思います。しかし，直方体の辺の長さの \(x \text{＋} y \text{＋} z\)，表面積の \(xy \text{＋} yz \text{＋} zx\)，体積の \(xyz\)という基本対称式を見て，\(x\)，\(y\)，\(z\) がそれらの値を係数とする３次方程式の3つの実数解であることに気づけば，実数条件の問題に帰着することもできます。
　グローバルトップの問題345は，後者の解法が有効です。一度触れておくことで，見抜きやすくなるタイプの問題でしょう。なお，2020年の長崎大学，2016年の同志社大学でも類問が出題されています。

　いかがでしたでしょうか。第2回は「確実に押さえたい練習が必要な問題」を取り上げます。お楽しみに！

※入試対策問題集『ニューグローバルトップ数学Ⅰ＋Ａ＋Ⅱ＋Ｂ＋Ｃ』の詳細は，こちらをご覧ください。