教科書・教材のひと工夫（高校）

　本記事では，2025年に出題された大学入試問題について，「思考の戦略編」で取り上げた思考法をもとに分析してみたいと思います。

東北大学（理系）　大問６

　(2)は，正五角形を角 \(\theta\) だけ回転させたとき，共通部分の周の長さを考える問題です。
　図形のイメージをつかむために，まずは \(P\) と \(P_{\theta}\) の図をかいてみましょう。

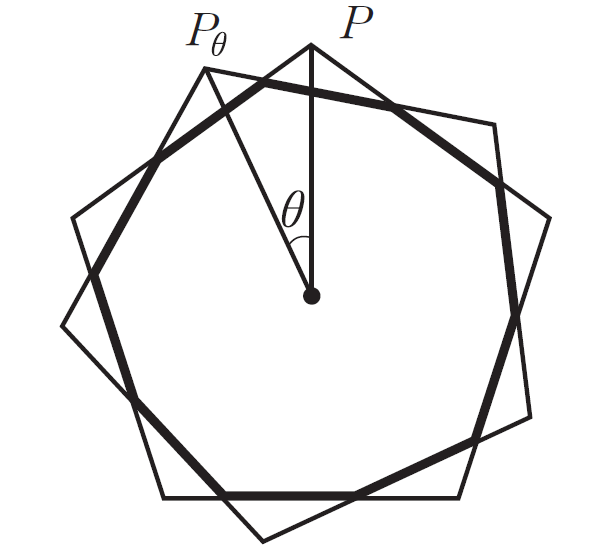
　共通部分は十角形になりそうですが，\(l_{\theta}\) を求めるために，10本の辺の和を考えるのは大変そうです。
　ここで，対称性に着目してみましょう。
　正五角形は外接円の中心のまわりに72°回転すると，もとの正五角形に一致するという対称性をもっています。よって，下の図のように点 \(\text{A，B，C，D}\) をおいたとき，\(P\) を \(K\) の外接円の中心 \(\text{O}\) のまわりに72°回転すると，点 \(\text{A}\) は点 \(\text{C}\) に，点 \(\text{B}\) は点 \(\text{D}\) の位置に移動します。
　ゆえに，\(\boldsymbol{P}\) と \(\boldsymbol{P_{\theta}}\) の共通部分は5つの合同な四角形からなり，\(l_{\theta}\) は \(\text{AB}+\text{BC}\) の長さを5倍すれば求められることが分かります。

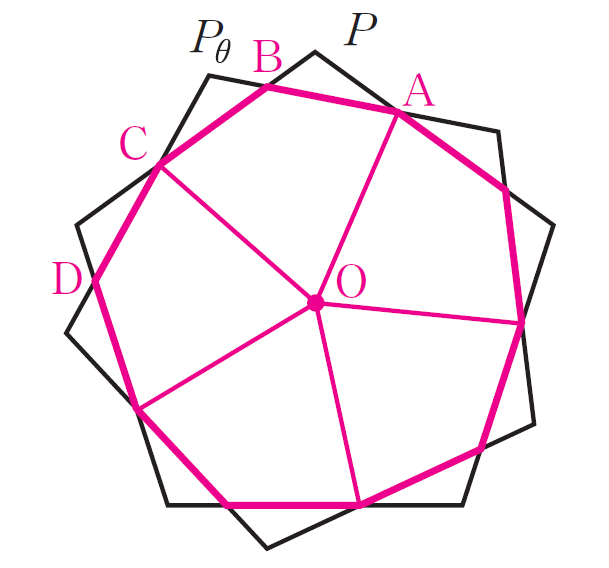
　さらに，\(\text{AB}\) と \(\text{BC}\) の長さについて考えてみましょう。
　\(P_{\theta}\) は \(P\) を \(\text{O}\) のまわりに角 \(\theta\) だけ回転して得られる図形ですから，点 \(\text{A}\) と点 \(\text{C}\) は線分 \(\text{OB}\) に関して対称な位置にあり，\(\text{AB}=\text{BC}\) となります（このことをしっかり証明するとこちらのようになります）。
　ゆえに，共通部分は正十角形であり，\(l_{\theta}\) は1辺の長さを10倍すれば求められることが分かります。
　したがって，まずは \(\text{AB}\) の長さを求めようと解答の方針を立てることができます。

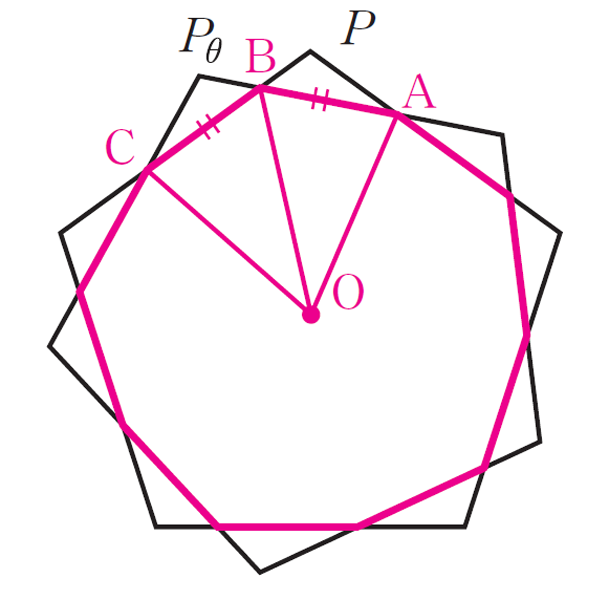
　このように，対称性に着目することで簡潔に考えることができるようになり，見通しよく解答を記述することができるようになります。
　この“対称性を利用する”という考え方は，『数学Ⅰ Advanced』，『数学A Advanced』の「思考の戦略編」で取り上げています。さらに，『数学Ⅰ Advanced』p.215の問6では，正方形を回転させ重なる部分の面積を求める，東北大の問題に近い内容を扱っています。

東京科学大学（理工学系：旧東京工業大学）　大問３

　(1)について考えてみましょう。
　まず，ゲームが終わったときに1点となっている確率 \(Q_1\) を考えますが
「1点でゲームが終わるのはどのようなときか」
→「1点加算され，その状態で2回続けて裏が出ればよい」
→「そのためには，裏が2回続けて出る前に，表が1回出ていなければならない」
と結果の状況から逆向きに考えることで，状況を整理することができます。

　次に，ゲームが終わったときに2点となっている確率 \(Q_2\) を考えます。
1点のときと同様に結果の状況から逆向きに考えることに加えて，(1)で考えた確率を利用すると簡潔に考えることができます。
「2点でゲームが終わるのはどのようなときか」
→「2点加算され，その状態で2回続けて裏が出ればよい」
→「そのためには，1点加算され，その状態で『1点加算され，その状態で2回続けて裏が出る』という事象が起こればよい」
と考えることができます。

　続いて，(2)では，ゲームが終わったときに \(n\) 点になっている確率 \(Q_n\) を考えます。\(Q_{n+1}\) と \(Q_n\) の関係から漸化式を立てることができれば，\(Q_n\) を求めることができそうです。
ここでも，(1)で考えたことを利用して，\(Q_{n+1}\) と \(Q_n\) の関係を \(Q_2\) と \(Q_1\) の関係と同じように考えてみましょう。
「\((n+1)\) 点でゲームが終わるのはどのようなときか」
→「\((n+1)\) 点加算され，その状態で2回続けて裏が出ればよい」
→「そのためには，1点加算され，その状態で『\(n\) 点加算され，その状態で2回続けて裏が出る』という事象が起こればよい」
と考えることで，\(Q_n\) についての漸化式を立てることができます。

　この問題では，やみくもに確率を考えるのではなく，結果の状況から逆向きに考えることで，状況を整理して見通しよく計算を行うことができました。
　この”逆向きに考える”という考え方は，『数学A Advanced』の「思考の戦略編」で取り上げています。

　2025年の入試問題について，“対称性を利用する”や“逆向きに考える”といった思考法を意識することで，解決の糸口を見つけることができることを紹介しました。
　Advancedの「思考の戦略編」では，教科書で学んだことを振り返りながらそのような思考法が身につく工夫を凝らしています。「思考の戦略編」が生徒の皆さんの思考力の向上に貢献できましたら幸いです。

関連記事はこちら

＞【改訂版教科書】LEGENDと同様の，分野を越えて共通する思考法を学ぶ （Advancedシリーズ）