教科書・教材のひと工夫(高校)
- TOP
- 教科書・教材のひと工夫(高校)
- 【改訂版教科書】豊富な「別解」で問題を多面的に捉え…


数学の問題では,1つの問題に対して複数の解法が考えられることがあります。
日々の学習のなかで複数の解法を意識していると,問題を多面的に捉える視点を身につけることができます。そのような視点が身についていると,難しい問題に対して,ある解法では解くことができなくても「別の解法ではどうだろうか?」と,さまざまなアプローチを試みることができるようになります。
日々の学習のなかで複数の解法を意識していると,問題を多面的に捉える視点を身につけることができます。そのような視点が身についていると,難しい問題に対して,ある解法では解くことができなくても「別の解法ではどうだろうか?」と,さまざまなアプローチを試みることができるようになります。
また,近年の大学入試では,「複数の解法を考えられるか?」が問われることもあります。
以下の問いに答えよ.
(1) \(\text{AB}=4\),\(\text{AC}=3\) である三角形 \(\text{ABC}\) の辺 \(\text{BC}\) を \(2:1\) に内分する点を \(\text{D}\) とする. また,\(\text{AD}=1\) とする。
(a) \(\text{BC}\) の長さを求めよ.
(b) (a)とは別の解法で \(\text{BC}\) の長さを求めよ.
(1) \(\text{AB}=4\),\(\text{AC}=3\) である三角形 \(\text{ABC}\) の辺 \(\text{BC}\) を \(2:1\) に内分する点を \(\text{D}\) とする. また,\(\text{AD}=1\) とする。
(a) \(\text{BC}\) の長さを求めよ.
(b) (a)とは別の解法で \(\text{BC}\) の長さを求めよ.
浜松医科大学(2021年)
このような実態に合わせて,改訂したAdvancedシリーズ,Standardシリーズでは,さまざまな箇所で,1つの解法だけではなく「別解」を示しました。
Advancedシリーズの「別解」
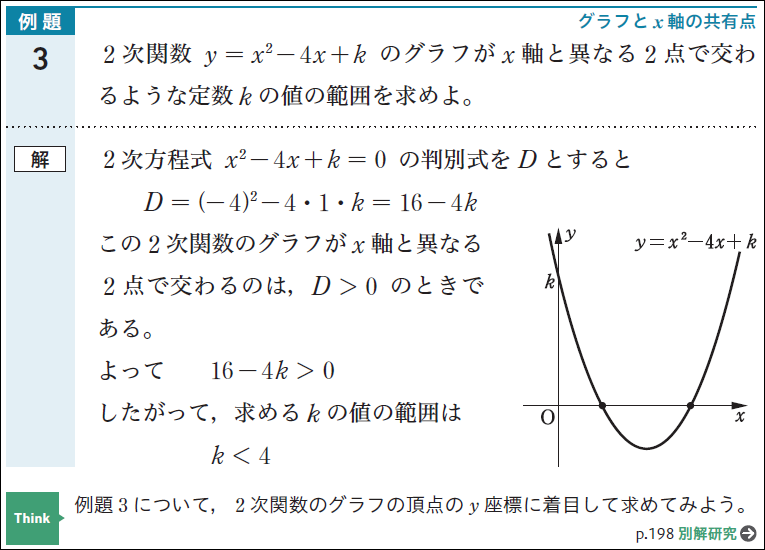
本文の例や例題中の解答の下に,授業のちょっとした時間でも紹介できる「別解」を示しています。生徒が自然に発想できる解法を,「別解」のアイコンをつけて目立たせることで,生徒が別解の存在を意識できるようにしました。(詳細はこちら)
Standardシリーズの「別解研究」
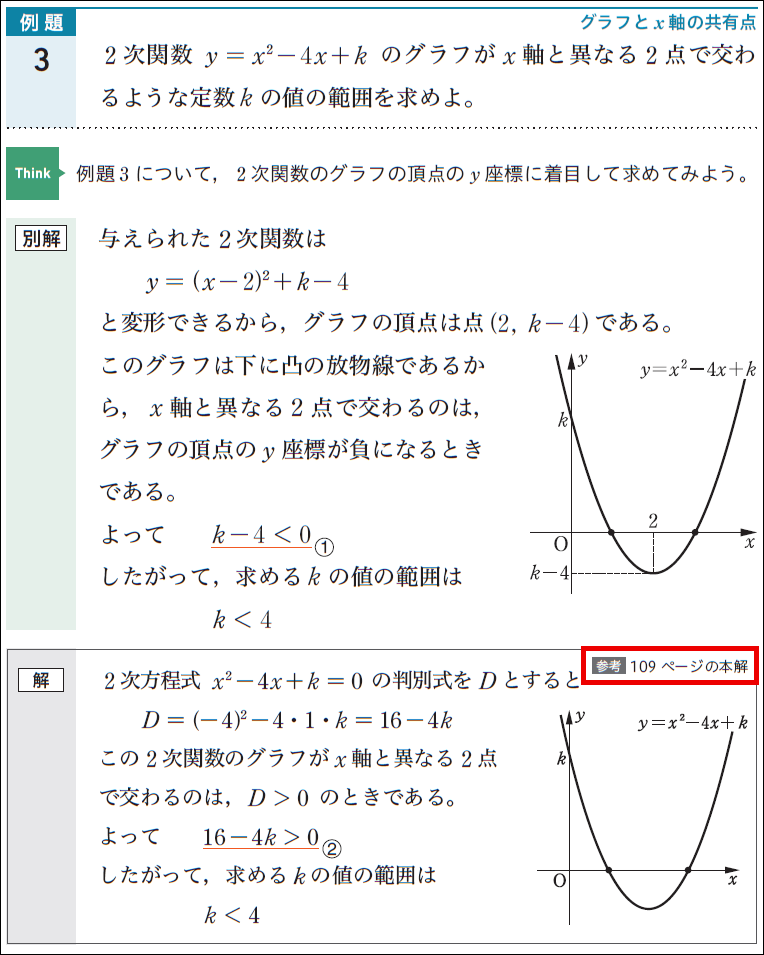
本文の例題の下で別解を考えさせる問いかけ(Think)を示し,巻末の「別解研究」で本解と別解を並べて示しています。巻末でまとめて確認することができるので,先生の授業の方針に合わせて自由にご利用いただけます。(詳細はこちら)

Advancedシリーズの「別解」,Standardシリーズの「別解研究」を日々の授業でご活用いただくことで,大学入試への素地作りをしてみませんか。
その他のコンテンツ