今日の授業のひと工夫（小中学校）

「新しい数学」1年6章p.214の「数学のまど」では、半径 \(r\)、弧の長さ \(l\) のおうぎ形の面積が \(S=\dfrac{1}{2}\ell r\) と表されることを紹介しています。直前に、例2を解く過程を通して、中心角 \(a^{\circ}\)のおうぎ形の面積を求める式 \(S=\pi r^2 \times \dfrac{a}{360}\) の \(\dfrac{a}{360}\) を \(\dfrac{\mathrm{(弧ABの長さ)}}{\mathrm{(円Oの円周)}}\) や\(\dfrac{\mathrm{(底面の半径)}}{\mathrm{(母線の長さ)}}\) におきかえて、中心角を求めなくても面積が求められることに触れています。

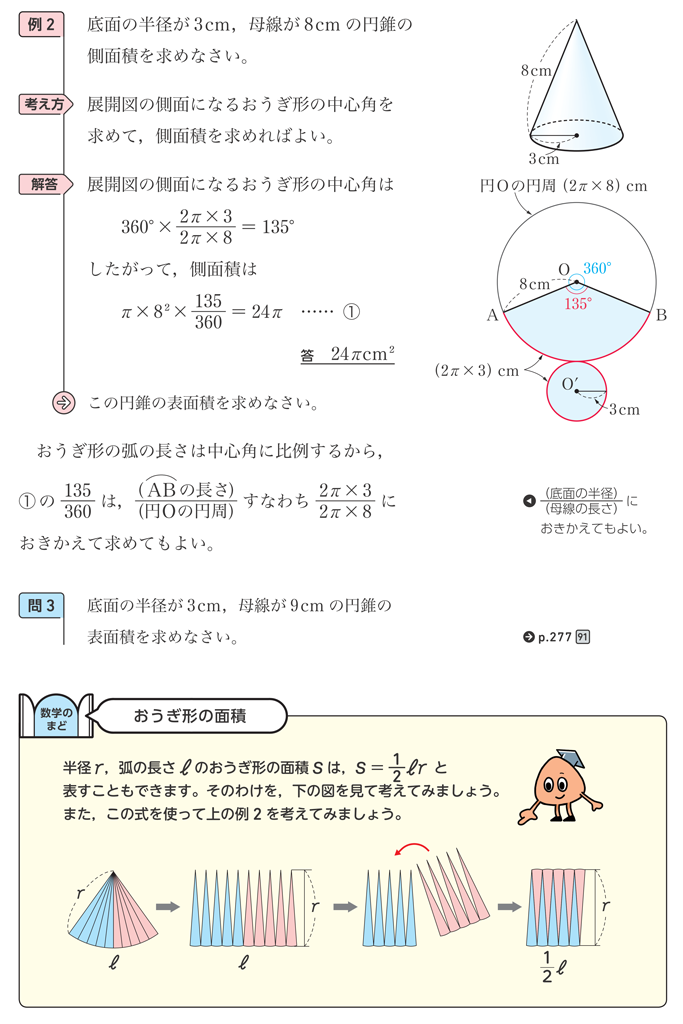
例2、問3で求めた円錐の側面積も \(S=\dfrac{1}{2}\ell r\) を利用して求めることができますね。「数学のまど」では、図を使ってこの式を直観的に理解させる扱いにとどめていますが、2年p.33章の問題B \(\boxed{ 4 }\) ではおうぎ形の弧の長さと面積の公式を利用して \(S=\dfrac{1}{2}\ell r\) となることを導きます。

ここで導いた等式 \(S=\dfrac{1}{2}\ell r\) の価値は、おうぎ形の面積を三角形の面積公式と同じようにみて求めることができるという点にあります。これは、三角形の面積の公式におうぎ形の面積の公式を統合したともいえますね。おうぎ形の中心角を小さくすれば、円周が直線に近づき、おうぎ形が三角形に近似されます。このことを見せると、等式の意味をより深く理解することが期待できますね。

さらに3年p.35 例2では、円形の土地を囲む道の面積は、（道幅）×（道の真ん中を通る線の長さ）、つまり \(S=a\ell\) となることを説明します。

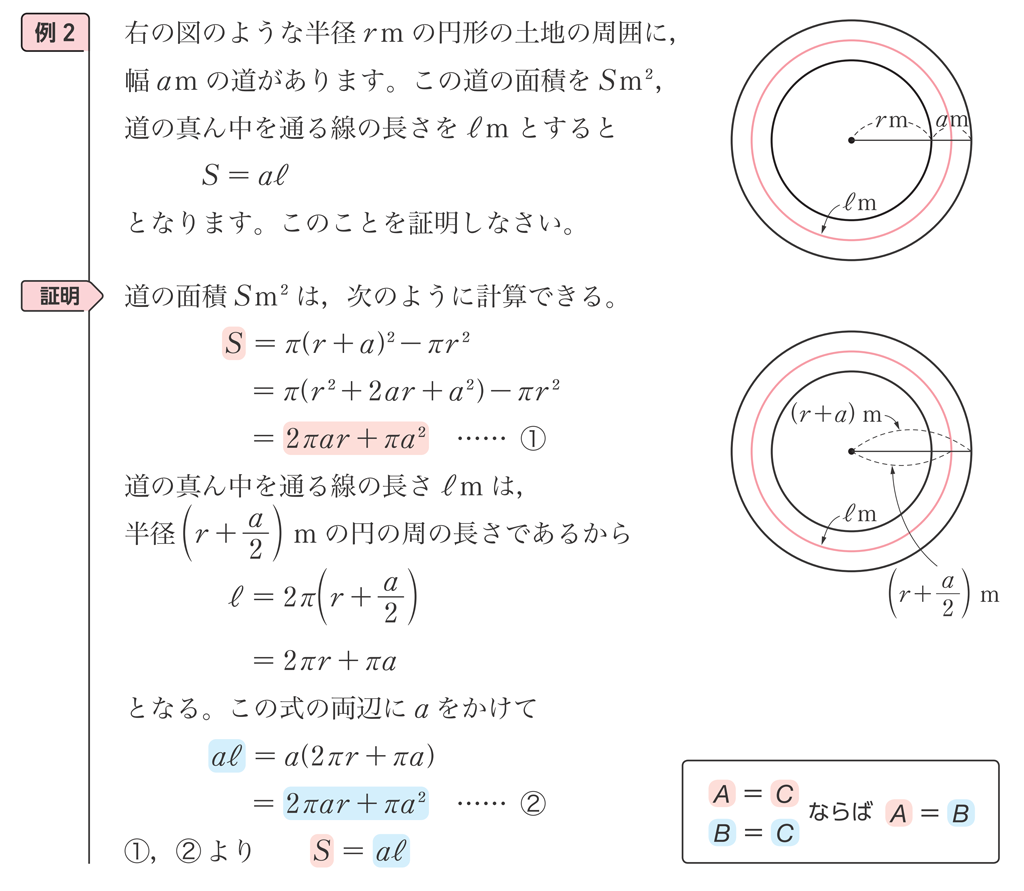
ここで、例2の上の図で \(r=0\) にした場合を考えてみます。このとき、道の形は円になります。したがって、統合的に考えると、円の面積も（幅）×（道の真ん中を通る線の長さ）で求められることがわかります。同様に、おうぎ形の面積についても、次の図のように考えることができます。

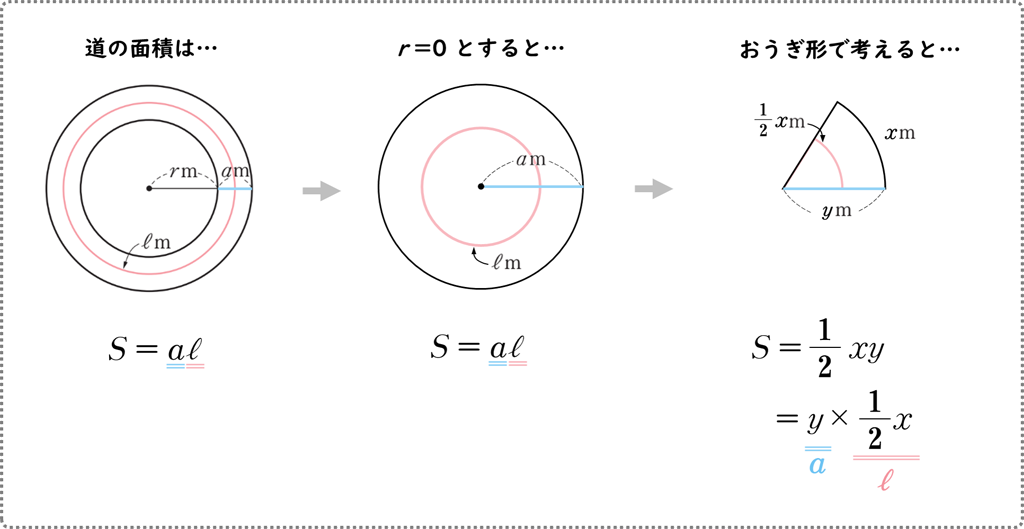
おうぎ形の面積の等式は、このように様々な見方ができます。それぞれの学年で適切に扱い、理解を深めたいところですね。