今日の授業のひと工夫（小中学校）

「新しい数学」2年5章p.147では、平行四辺形になるための条件を使って、図形の性質を証明します。これまでに、平行四辺形になるための条件の証明を扱い、「2組の対辺が平行」を結論として示すことを考えてきたため、ここでも、同じように「AE\(/\!/\)FC、AF\(/\!/\)EC」を示そうと考える生徒がいるでしょう。それを認めながらも、平行四辺形になるための条件\(\boxed{ 2 }\)～\(\boxed{ 5 }\)を根拠として利用してよいことを確認したいところです。

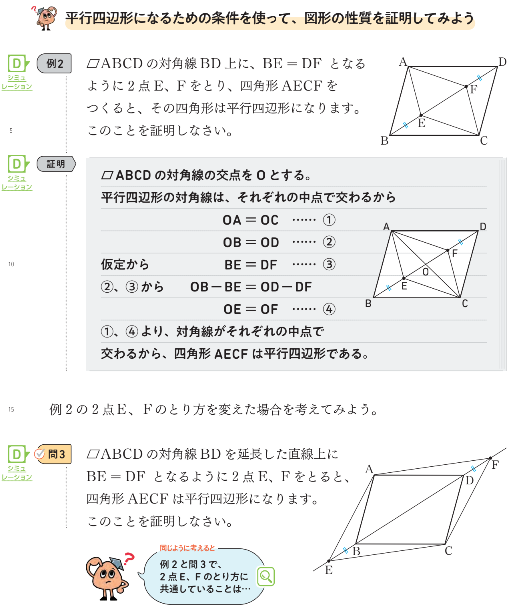
例2と問3はともに□ ABCDの対角線BD上またはBDの延長線上に、BE\(=\)DFとなるように2点E、Fをとり、四角形AECFが平行四辺形になることを示す問題です。問3の証明のあと、ルーローさんの吹き出しをきっかけにして、例2の証明と問3の証明を見比べて、共通点や相違点を明らかにしていきましょう。

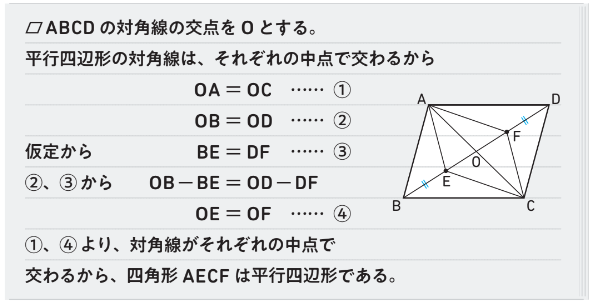
2つの証明の相違点は、例2では、OB\(-\)BE\(=\)OD\(-\)DF となっていますが、問3では、OB\(+\)BE\(=\)OD\(+\)DF となっている点で、それ以外は同じになっていますね。この2つの問題の考察を通して、「平行四辺形という点対称な図形に対して、点対称な位置で、同じ操作（同じ長さをたしたりひいたりする操作）をして得られた図形は、点対称な図形になる」ということがわかります。このことをはるかさんの吹き出しにふれて、生徒と一緒に考えてもよいですね。

これらの問題の解決では、1つの命題を証明したあと、問題の条件を変えて証明をふり返る活動を行いました。この活動を通して、統合的・発展的に考察する態度が育成されることが期待されますね。