今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【3年4章】関数 \(y=ax^2\) のグラフを…

ここでは、関数 \(y=ax^2\) のグラフのいろいろなかき方を紹介します。授業の中で取り上げてみると、生徒が興味を持つかもしれませんね。
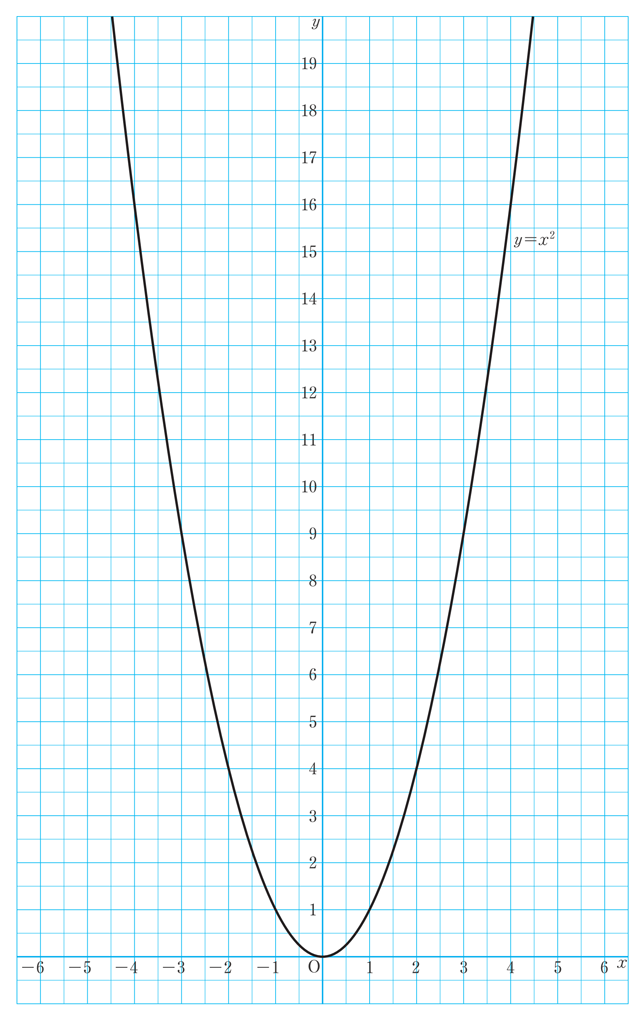
【方法1】方眼を利用したかき方
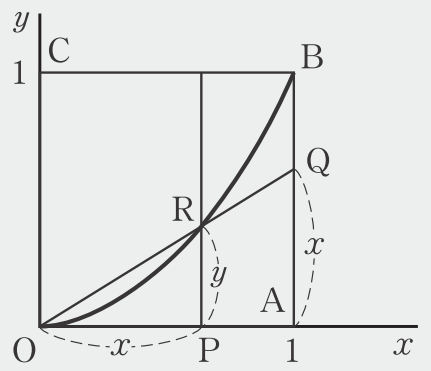
1辺の長さが1の正方形OABCの辺OA、AB上に、点P、QをOP=AQとなるようにそれぞれとり、Pを通りOCに平行な直線をひいて、直線OQと交わる点をRとすると点Rは \(y=x^2\) 上の点となります。
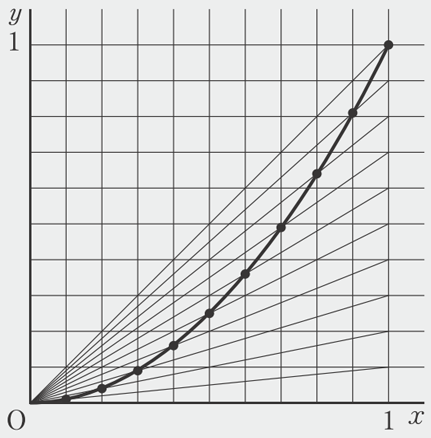
このことを利用して、下の図のようにして、点Rをたくさんとり、それらを順に結ぶと、\(y=x^2\) のグラフをかくことができます。
また、\(y=ax^2\) のグラフをかくには、1辺の長さが \(\frac{1}{a}\) の正方形をかいて、上と同じような操作をすればかくことができます。「三角形と比の定理」を学習する際にこの方法をふり返り、関数と図形を関連づけることも考えられますね。
【方法2】相似を利用したかき方
\(y=ax^2\) のグラフと \(y=x^2\) のグラフは相似になります。この相似を利用して \(y=ax^2\) のグラフを次のようにかくことができます。まず、\(y=x^2\) のグラフをかき、原点からの距離を \(a\) 倍した点をとる作業をくり返します。その点を結ぶと \(y=ax^2\) のグラフになります。
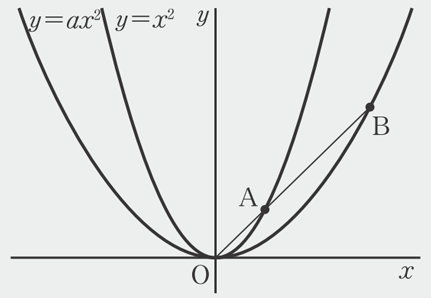
たとえば、\(a=3\) のときのグラフをこの方法を使ってかくと、このグラフ上の点が \(y=3x^2\) のグラフ上にあることが点の座標を読みとることで確認できます。
【方法3】折り紙を折る方法
折り紙の中に、点を1点取ります。点と折り紙の一番下の辺が重なるようにして折り、折り目をつけて戻します。これを何回もくり返すと折り目から放物線が浮かび上がります。


その他のコンテンツ
