
例えば,4個入り2箱,6個入り1箱だと,14人に1人1個ずつ配布できます。
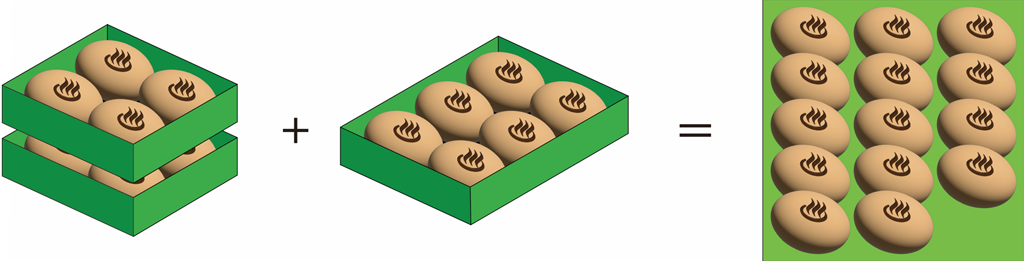
11人に1人1個ずつ配布するには何を何箱ずつ購入すればよいでしょうか?

【答】疑問を解決するために次のような数表をつくってみましょう。
ステップ1:4,6,9の中で一番小さい4を一段あたりの数字の個数として,0から適当な数まで4つずつ数字を並べる。そして,0と4,6,9の倍数に〇をつける。

ステップ2:6の列の6より下は,6に4の倍数を足した数になっていて,それらに〇をつける。

ステップ3:9の列の9より下は,9に4の倍数を足した数になっていて,それらに〇をつける。

ステップ4:15と15より下は, 6に「9と9より下」を足した数になっていて,それらに〇をつける。

ステップ5:以上をまとめると12以上はすべて〇がつけられる。
また,4,6,9の組み合わせでつくることのできない最大の数は11であることがわかる。

【答の深堀り】 この11を \((4,6,9)\) の三つ組のフロベニウス数(Frobenius number)と呼びます。
これを次のように表すことにしましょう。
\(F(4,6,9)=11\)
フロベニウス数がわかれば,それより大きい人数であれば何人であっても1人1個配布することができます。
【チャレンジ!】 某ハンバーガー店のチキンナゲットは,一時期,米国で6個入り,9個入り,20個入りの3種類のパックが販売されていたそうです。\(F(6,9,20)=43\) です。一段が6個の数表をつくってチャレンジしてみてください。 日本でも,1980年代には,5個入り,9個入り,16個入りの3種類のパックが販売されていたようです。\(F(5,9,16)\) を求めてみましょう。
もっと,大きな数の組で,\(F (11, 13, 23)\) も求めてみましょう。(答はページの一番下)
フロベニウスの贈り物
フロベニウスは1849~1917年に活躍したドイツの数学者です。ペロン-フロベニウスの定理など,フロベニウスの名前を冠した定理や専門用語は多いです。
フロベニウスは大学の講義中にしばしば次の問題を出題したようです。
『互いに素な正の整数 \(a_1,a_2, \ …,a_n\) に対して,これらの(0以上の整数を用いた)組み合わせで書けない最大の数は何か』
これは正に,今で言うフロベニウス数 \(F(a_1,a_2, \ …,a_n)\) を求める問題です。
今回の話は,まんじゅうに例えてつくりました。一般には「フロベニウスの硬貨交換問題」と呼ばれています。例えば,2円玉と5円玉しかなかったら3円はつくれません。4円玉と7円玉しかなかったら17円はつくれません。
2種類の場合はフロベニウス数を求める公式が知られています。
\(F(a,b)=(a-1)(b-1)-1\)
この公式はシルベスターにより与えられました。(1882年)
しかし,\(F(a,b,c)\) や \( F(a,b,c,d)\) など変数が3つ以上の場合の公式はいまだに知られていません。未解決問題です。もしかしたら,公式はつくれないのかもしれません。このような問題は代数学の,特に数値半群を研究している分野に関わっています。
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
【答】\(F (5, 9, 16) = 22\),\(F (11, 13, 23) = 64\)
※Wolfram Alphaの計算サイト(外部サイトにリンクします)で答を出してくれます。
フロベニウス数 [11,13,23]
と入力すると・・・。
その他のコンテンツ
