特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【#32】若手先生の困り事相談~令和6年度全国学力…
中学校
2024.11.28
【#32】若手先生の困り事相談~令和6年度全国学力・学習状況調査の結果を生かした授業づくり④~

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。
今回は、若手の先生からいただいた困り事について、考えてみたいと思います。
令和6年度全国学力・学習状況調査の結果を生かした授業づくり④

Q 令和6年度全国学力・学習状況調査問題の図形の問題をみて、これを題材に授業ができないかなと思いました。調査問題を活かした授業づくりのポイントを教えてください。
A 全国学力・学習状況調査問題の結果を活かすことは大切ですが、調査問題を題材として授業をつくり実践することも大切なことです。そのためには、調査問題を生徒の問題発見・解決の過程として検討し、授業のデザインをする必要があります。
前回は、令和6年度全国学力・学習状況調査問題大問9(1)の証明について取り上げ、調査結果からわかる指導改善のポイントについて考えました。
今回は、この大問9を取り上げ、これを用いて授業を行う際の授業デザインの進め方について考えてみましょう。ポイントは、「予想する―行動する―振り返る」ことを通した数学的な問題解決の場面づくりを考えることです。
□育成する資質・能力を明らかにするために調査問題を読み解く〜予想すること〜
大問9は、2つの設問を通して図形を考察する場面を設定しています。まず、設問(1)における「〜予想する〜」を考えみましょう。
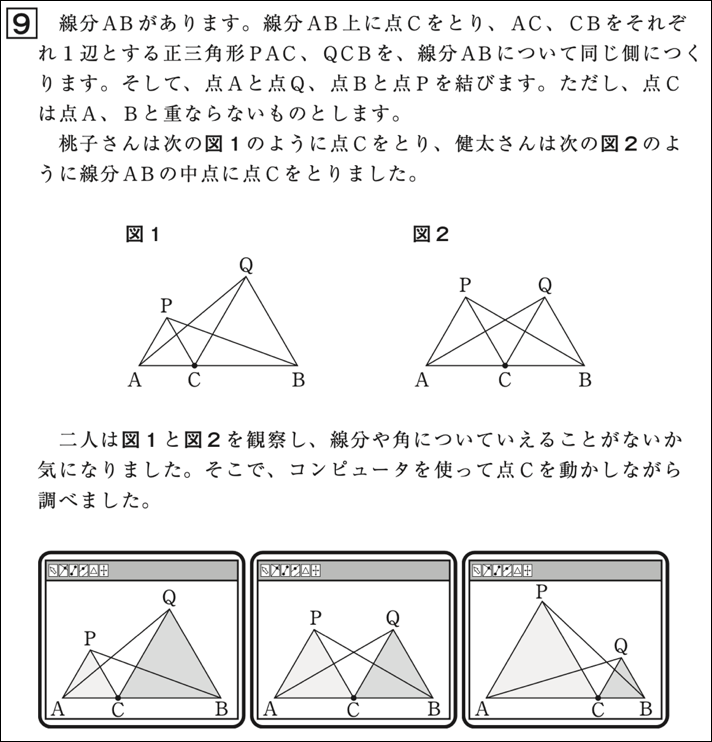

令和6年度全国学力・学習状況調査問題大問9(1)
(1)は、図形の証明問題です。中学校数学大問9(1)については、前回も取り上げたように「予想した事柄が成り立つことを論理的に考察し表現すること」を評価する設問です。調査結果から、指導改善のポイントについてお伝えしました。証明を書くことに拘らず、筋道を立てて考えることを表現することに力点をおいた指導が必要です。
実際の授業では、最初から証明の問題を提示するのでなく、考察の文脈を考える必要があります。(1)の設問では、問題設定までに1ページを費やし、問題解決の入り口を丁寧に表現しています。よく読解力という言葉を例に、問題文を読むことができるか・できないかということを心配される先生がいます。確かに、書かれていることを読むことは大切なことです。最初のページには、①解決の対象となる図の設定(前提)が示されています。特に点\(\text{C}\)を線分\(\text{AB}\)上を動かし、図を動的なものとして提示しています。もちろんPBT(Paper-Based Testing)ですので、伝える情報としては静的なものになってしまうのは仕方がありません。しかし、授業では工夫ができます。問題文において「コンピュータを使って調べました」とあるように、生徒一人一人がコンピュータを利用して、図形を動的なものとして実際に操作して観察する場面づくりが大切です。ここで、気をつけたいことは、コンピュータを使用することが目的ではなく、生徒がこの事象に数学的な予想、成り立つと予想される事柄を見いだす場面につなげることです。生徒はどのような事柄を予想するでしょうか。下のように、“変わるもの”と“変わらないもの”として発問することは有効です。この設問で変わらないものは「\(\text{AQ=PB}\)」ですが、この他にも考えることが想定されますね。例えば、辺や角の大きさの相等関係、合同な2つの三角形の組など。先生が証明してほしいことを押しつけることなく、証明の対象となる事柄を学級で絞っていくことも大切です。
<想定される教師と生徒ととのやりとり>
| 先生: | 線分\(\text{AB}\)の中点の位置にとった点\(\text{C}\)を、線分\(\text{AB}\)上で動かしてみました。点\(\text{C}\)を動かしたときこの図において、“変わるもの”や“変わらないもの”はありますか?話し合ってみましょう。 |
| 生徒: | \(\triangle \text{PAC}\)の大きさ(面積)は大きくなったり、小さくなったりします。 |
| 生徒: | \(\triangle \text{QCB}\)にも同じようなことがいえる。 |
| 生徒: | 辺や角の大きさもそうだ。 |
| 生徒: | “変わらないもの”なんてあるのかな? |
| 生徒: | 中点\(\text{M}\)は変わらないよ。 |
| 先生: | そうですね。では、“何かと何かとの関係”についてはどうでしょうか。 |
| 生徒: | 関係?辺と辺とか? |
| 生徒: | もう一回、図をみてみよう。 |
図を動的にみているので、“変わらないもの”を探すことは困難に感じる生徒もいます。上のようなやりとりを通して、関係に着目できるように教師が支援しながら、「〜予想する〜」場面を授業にどのようにして設定できるかを考えましょう。
次回以降では、設問(2)での「予想する―行動する―振り返る」を取り上げ、調査問題を活かした授業づくりを考えます。
※参考資料
- 令和6年度全国学力・学習状況調査解説資料中学校数学(国立教育政策研究所)
- 令和6年度全国学力・学習状況調査報告書中学校数学(国立教育政策研究所)
【佐藤寿仁先生 略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。
東京書籍では、先生方の困り事を募集しています。
日々の校務のなかのさまざまな困り事を、教科書に携わっている経験豊富な先生から解決のアドバイスやヒントをいただいてみませんか。
困り事は、こちらのGoogleフォームからお送りください。
(すべての困り事に対して、回答できかねますことをご了承ください。)
その他のコンテンツ
