特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

「個別最適な学び」と「協働的な学び」の一体的な充実を考える④

Q　単元の中盤では、知識や技能の内容が中心で、一方的に学習内容を伝えるような授業となってしまいます。単元の中盤に「個別最適な学びと協働的な学びの一体化」をどのように取り入れるとよいのでしょうか。

Ａ　単元の中盤では、「知識・技能」を評価することが多くなります。「知識及び技能」の授業では、生徒が学習を通して、概念を獲得することが大切です。そこで、数学的な見方・考え方を働かせて概念を追究する場面を設定し、「個別最適な学びと協働的な学び」を授業に取り入れましょう。

　前回は、「個別最適な学びと協働的な学びの一体化」を単元全体で考え、その上で、単元の指導計画を検討することをお話しました。また、単元の導入では、学習の個性化を図るため生徒一人一人が単元の問い（＝学習課題）を持つことが大切であるとしました。今回も「新しい数学3」の関数領域、「第4章 関数の世界をひろげよう［ \(y=ax^2\) ］」の指導場面を例とします。まず、前回取り上げた単元の指導計画をについて表に示します。

表　単元の指導計画と生徒の問題解決について

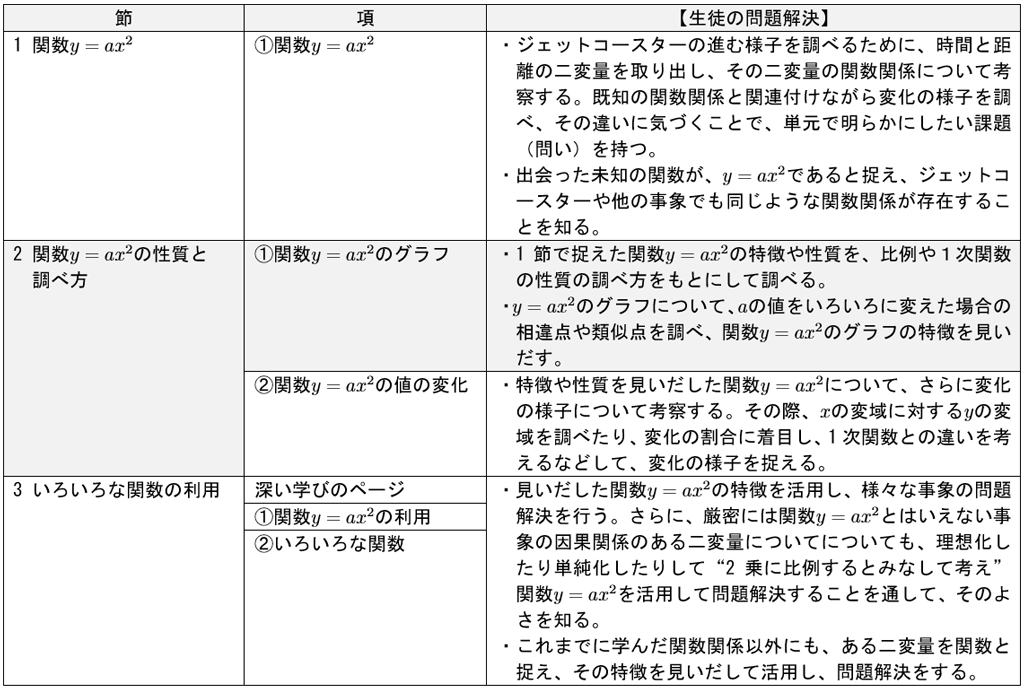
□「個別最適な学びと協働的な学び」を取り入れ、概念追究型の授業を計画する

　前回#27では、単元の導入場面において持つ生徒の学習課題についてお話しました。その中で、「ジェットコースターが動く様子は、1次関数（比例）や反比例とは異なる関数関係だろうか？」「その関数は、どんな式に表せるのか？どんなグラフになるのか？」などの学習課題を例としました。「どのような関数関係なのか？」という学習課題について、個人で、または、グループで追究することが考えられます。教科書の進め方のようにグラフ、変化の割合の順に進めていくこともよいでしょうし、大きなテーマである程度の時間を生徒が取り組むことも考えられます。

　具体的には、第2節において「関数 \(y=ax^2\) のグラフは、どのようなグラフになる？」と学級の学習課題を確認したあと、「どのように調べればよいでしょうか」と方法を投げかけることが考えられます。個や集団で、見通しを立てたり、これまでの学びをふり返ったりしてグラフの特徴の調べ方を考えさせてみましょう。子どもたちの見通しが立ったところで、関数 \(y=ax^2\) の \(a=1\) のときのグラフについて検討します。その後、生徒自身で \(a\) の値を変えて、グラフをかいて考察するとよいでしょう。また、最初から \(a\) の値を自分で決めて活動できる生徒がいる一方で、促されても自分で \(a\) の値を設定することができない生徒もいます。そのときには「\(a\) の値をまず \(2\) とするのはどうか」などと具体的な数で促すことで、その後 \(\dfrac{1}{2}\)、\(-2\)、\(- \dfrac{1}{2}\) など分数や負の整数に拡げて考えることを支援するとよいでしょう。考察を生徒1人で進めることに固執せず、ペアやグループでの活動場面を設定し、個と集団での考察の行き来を活発にします。このとき、教師は生徒と一緒に考える姿勢を持ち、生徒の学びに伴走することを大切にしましょう。

　「新しい数学3」のDマークコンテンツにはシミュレーション「関数 \(y=ax^2\) のグラフを調べよう」が用意されています。生徒の端末を用いて、個人や集団での追究する場面に使用することが考えられます。関数 \(y=ax^2\) の \(a\) の値を変えたとき、それに対応するグラフの形を観察し、わかったことや気づいたことをグループで共有することで、関数 \(y=ax^2\) のグラフの特徴を生徒自身で検討することができるでしょう。

Dマークコンテンツ「関数 \(y=ax^2\) のグラフを調べよう」

［https://tsho.jp/03j/m3/］

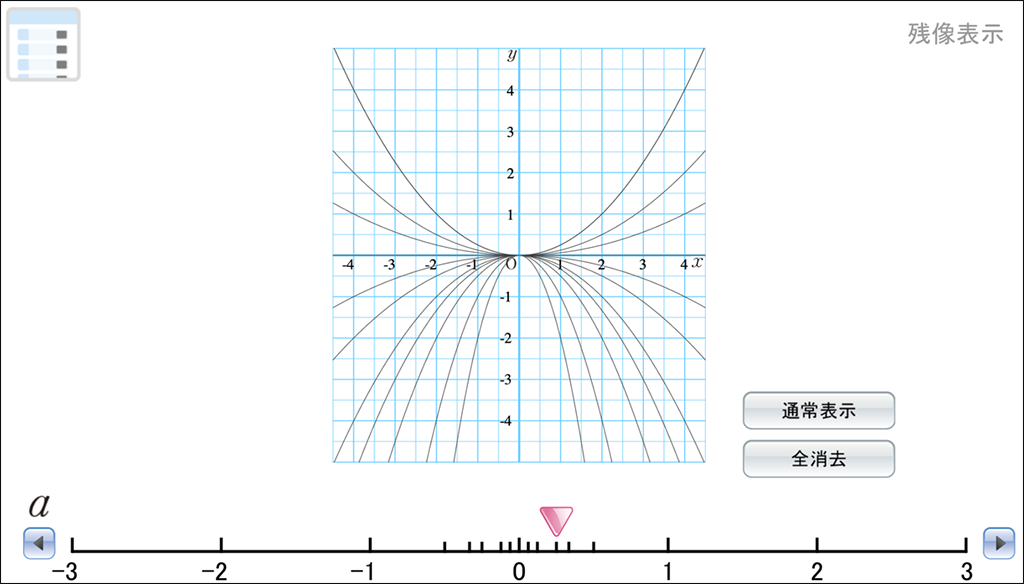
　単元の中盤では、学習内容を伝える指導でなく、単元の導入時に生徒が持った単元の問いを学習課題に結び付け、個別と集団での学習を相互に関わらせながら、概念を追究する授業を行うことが大切です。

QRコンテンツ「関数 \(y=ax^2\) のグラフを調べよう」はこちら

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。

※参考資料

• 「令和の日本型学校教育」の構築を目指して～全ての子供たちの可能性を引き出す，個別最適な学びと，協働的な学びの実現～（答申）　令和3年1月26日（中央教育審議会）
• 新しい数学3（東京書籍）
• 「新しい数学」学習指導計画（略案）【3年】

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。