特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

「個別最適な学び」と「協働的な学び」の一体的な充実を考える②

Q　数学の授業に「協働的な学び」として話し合って進める学びの場面を設けています。この場面での授業づくりのポイントを教えてください。

Ａ　「協働的な学び」というと、授業において生徒どうしで話し合う場面を設定することが見られ、それを学びあいとして取り入れる授業が見られます。そのとき、何を話し合えばよいのかなど数学の指導目標にあわせて話し合う内容を考えることが大切です。

　前回から「個別最適な学び」と「協働的な学び」を考えた中学校数学の授業づくりについてお話しています。前回は「個別最適な学び」にフォーカスし、指導の個別化と学びの個性化について具体的な数学の授業場面で考えてみました。

□「協働的な学び」を授業に取り入れる

　「個別最適な学び」と「協働的な学び」は、文部科学省が2021年1月に中央教育審議会の答申で公表された「令和の日本型教育の構築」という中で公表されたものであることは【#25】でお伝えしました。以前の学習指導要領では、思考力、判断力、表現力を重視し、「言語活動」が求められました。そこで、授業では積極的に「話し合う場面」が設定され、それをグループ活動と称して実践されました。ところが、校内外での授業研究会において、「何人で話し合うのか」、「机をどう向き合わせるとよいか」といった教科教育から少し離れた議論がなされ、言語活動のための本質的な指導法について、あまり取り上げられていなかった現状があったと思います。生徒が複数人でグループを組み、にぎやかに話をしていることでグループ活動が成立している、としてしまっていたのではないでしょうか。
　【#25】で取り上げた「新しい数学2」の第2章「連立方程式」（p.47）の例2では、これまでの学習を生かしながら、解く方法を考えたときに式を組み合わせて2つの二元一次方程式をつくります。

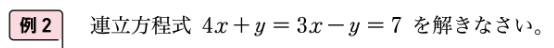
新しい数学2 第2章「連立方程式」p.47

　生徒は問題解決のための見通しを自ら持ち、行動する（自力解決）ことで
「\(\text{A}=\text{B}=\text{C}\) の形の連立方程式」の解き方を考えます。その後、「\(\text{A}=\text{B}=\text{C}\)」から「\(\text{A}=\text{B}\)、\(\text{A}=\text{C}\)」「\(\text{A}=\text{B}\)、\(\text{B}=\text{C}\)」「\(\text{A}=\text{C}\)、\(\text{B}=\text{C}\)」のような組み合わせをつくって、どの組み合わせでも同じ解が得られることを確認するでしょう。この授業における「協働的な学び」として、下のように様々に考えることができます。

• 式の組み合わせについて話し合う
• 組み合わせてできた連立方程式の解法を話し合う
• それぞれで考えた式の組み合わせと解法について共有し、「\(\text{A}=\text{B}=\text{C}\) の形の連立方程式」の解法について検討するために話し合う

　他にもあるかもしれませんし、どれが正解というわけでもありません。授業者が何を本時の指導目標としているのかによります。私なら、ここでは下のようなことを話し合いによって見いだしてほしいと考えます。

1. 「\(\text{A}=\text{B}=\text{C}\) の形の連立方程式」はそのままでは解くことができないが、
   「\(\text{A}=\text{B}\)、\(\text{B}=\text{C}\)」のように組み合わせて考えることで解くことができるようになること
2. どの組み合わせでも解くことはできるが、式の操作や処理に違いがあり、自分が進めやすい式の組み合わせをつくることが大切であること
3. 上記1や2のいずれにしても、操作や方向性を自分で考えることが大切であること

　「協働的な学び」は、話し合う場面を設定することではなく、その学習内容の本質的な理解を促すための活動につなげる学びである必要があります。そして、この活動を通して学びは深まり、「深い学び」につながっていくのでしょう。深い学びである「学びの本質」は、教師が教材研究を通して見いだすものですので、学習指導要領の解説で確認するだけでなく、使用する教科書をよく読み解くことも大切です。

※参考資料

• 「令和の日本型学校教育」の構築を目指して ～全ての子供たちの可能性を引き出す，個別最適な学びと，協働的な学びの実現～（答申）　令和3年1月26日（中央教育審議会）
• 新しい数学2（東京書籍）

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。