特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

「個別最適な学び」と「協働的な学び」の一体的な充実を考える①

Q　授業づくりに「個別最適な学び」と「協働的な学び」が大切だと言われています。どのようなことを考えて授業づくりに取り組むとよいのでしょうか。

Ａ　学校、教室での学びでは、個と集団のダイナミックに交わることにより学びが展開されることが期待されます。「個別最適な学び」と「協働的な学び」がそれぞれ何を指すのかを確認しながら、それらの成果が互いの学びにどのように生かされるかを考え、資質・能力の育成を目指すことが大切です。

　新学期がスタートして約2ヶ月が経ちました。新しい学級や学年に慣れ、先生方は学習環境を整え、日々の授業づくりとその実践に取り組まれていることと思います。中学校では、単元のテストや学期末のテストなどの取り組みもあるのではないでしょうか。
　さて、今回から「個別最適な学び」と「協働的な学び」を考えた中学校数学の授業づくりについて考えます。

□資質・能力の育成を目指した子どもの学び方の充実

　「個別最適な学び」と「協働的な学び」は、文部科学省が2021年1月に中央教育審議会の答申された「令和の日本型教育の構築」の中で公表された子どもの学びに関するものです。これまでの日本の学校教育の成果を評価しながらも、今後の社会を想定し、子どもたちが社会の創り手となれるような学びのアップデートについて示されました。その中で、各学校に対して「個別最適な学び」と「協働的な学び」の必要性について説明されています。子どもの学び方は様々に考えられ、これまでも多くの方法が研究され、学校で実践されてきました。どの方法がよいのかではなく、資質・能力の育成が確実になされることが大切であり、今回取り上げた「個別最適な学び」と「協働的な学び」についても、その言葉だけが一人歩きすることなく、子どもにとってよいものとなることを考えなければなりません。
　この2つの学びについて、文部科学省は「個別最適な学び」と「協働的な学び」については、常に“一体的な充実”として述べています。つまり、「『個別最適な学びと』と『協働的な学び』の一体的な充実」としてこの言葉は示されたのです。しかし、考えてみればそれは当たり前のことであり、学校での子どもの学びは、子ども一人一人に応じた学習活動もありますし、一人一人の考えを共有したり、組み合わせたりして問題解決をすることを通した学習活動もあります。つまり、現在の学校の学習環境、育成を目指す資質・能力を踏まえ、個と集団の学びを捉え直し、その結びつきを有機的なものとして考え整理したことを、よい授業をつくるための考えとして公表されたのです。そして、このことは授業改善の視点である主体的・対話的で深い学びの実現にもつながるものです。
　こうしたことを踏まえて、まず「個別最適な学び」について考えてみましょう。

□「個別最適な学び」とはどのような学びをいうのか

　子どもの興味・関心を生かした自主的、主体的な学習を促し、一人一人の学習状況に応じた指導は「個に応じた指導」として、これまでも学校で丁寧にされてきました。数学の内容の理解には個人差がありますので、理解の程度や状況に応じて取り組む問題を設定することがあります。例えば、「分数が含まれる方程式」を解くことに困難があれば、「分数の計算」「分数の通分」「等式の変形」などの、それにつながる課題を用意して、個別に指導することがあると思います。こうしたことは、指導の個別化（個別指導）と呼ばれ、実践されてきました。日本の先生は子どものことを考え、このような指導を熱心に取り組んでいるといえます。たいへん素晴らしいことです。
　総合的な学習の時間のような探究プロセスがあるような学習では、自分事の課題を持ち、解決の計画を立てて実行し、問題解決をしていくことが求められます。このとき、問題そのものを自分で発見し、解決に向かいます。子どもが自分で課題を見いだして問題解決する学習においては、学習者の一人一人がフォーカスされる学びとなり、これを学びの個性化と言われています。ICTの活用で子ども一人一人が端末を使用きるようになったことで、こうした活動はますます求められてきていると思います。

□数学の授業における「個別最適な学び」を考える

　「個別最適な学び」は、指導の個別化と学びの個性化の2つがあり、どちらか一方が大切であるとか、バランスをとって行うというよりも、学習者である子ども一人一人を大切にするためにあることを確認しましょう。令和の日本型学校教育においては、学校教育で“誰一人取り残すことのない”ことが強調されています。
　では、中学校数学の授業で考える「個別最適な学び」の具体について考えてみましょう。「佐藤寿仁先生と考える【#23】【#24】」では「知識及び技能」の育成に関わって、文字と式での指導についてお伝えしました。そこでは、式の計算方法を自ら考え、試して計算方法を見いだすという内容のお話でした。数と式の領域においては、後の学習や何らかの問題解決に活用することを想定すると、的確に計算できるようになることも大切です。「新しい数学2」の第2章「連立方程式」（p.43）では連立方程式を一方の文字を消去するために加減法を用いて解くことができるかどうかを評価する内容があります。

新しい数学2 第2章「連立方程式」p.43

　この例題について、授業では学級で解法を考え、前ページにある例2を振り返りながら解法を検討し、それを明らかにする活動が想定されます。例3の後には、「問3」が用意されています。

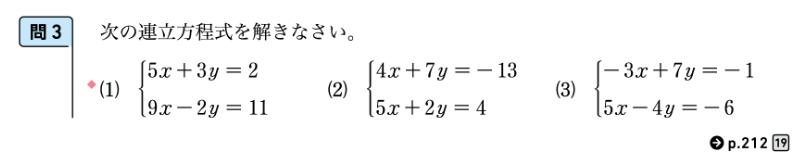
新しい数学2 第2章「連立方程式」p.43

　（1）は◆マークがついていますので、直近の例3の連立方程式と係数は異なりますが、同じ構造になっている意図された問題設定です。簡単なようにみえますが例3と同じようにして取り組むことができない生徒もいると思います。一方で、（1）〜（3）までの連立方程式をすぐに解くことができる生徒もいるでしょう。問3の右下には“→”のマークがあります。これは補充問題へのリンクです。さらに理解を深めるために、その問題へのチャレンジを促すとよいでしょう。いずれも子どもの学習状況を個別に想定した際の教師の取り組みであり、生徒に様々な状況に寄り添って指導することが、指導の個別化といえます。
　では、学びの個性化についてはどうでしょう。数学の授業では、事象や問題が既に設定されていることがほとんどですので、総合的な学習の時間のように自分で問題そのものを考える機会は少ないかもしれません。
　例えば、「新しい数学2」の第2章「連立方程式」（p.47）の例2をみてみます。

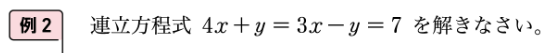
新しい数学2 第2章「連立方程式」p.47

　例2は、問題解決としては「連立方程式の解を求める」になりますが、評価としては解く方法を考え、説明するという「思考力、判断力、表現力等」を設定するのではないでしょうか。ここでは、これまでの学習を生かしながら、式を組み合わせて2つの二元一次方程式をつくります。このことを教師が一方的に教え伝えるのではなく、生徒自らの主体的な取り組みを期待します。組み合わせは、複数ありますので、それらを自ら考え選択し、問題解決に向かっていくことは、学習者それぞれの見通しとその活動を保障するものであり、学びの個性化にもつながるものではないかと考えます。
　しかし、個人で様々な方法で取り組み、たとえ解決ができたとしても、そのまま授業が終わってしまえば、学びは深まりません。ここでは集団での交わりが必要で、協働的な学びの出番となるのです。
　次回は、「協働的な学び」について考えましょう。

※参考資料

• 「令和の日本型学校教育」の構築を目指して ～全ての子供たちの可能性を引き出す，個別最適な学びと，協働的な学びの実現～（答申）　令和3年1月26日（中央教育審議会）
• 新しい数学2（東京書籍）

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。