特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

図形の証明における指導を考える③ 〜アセスメント（学習評価）〜

Q　生徒が図形の証明を書くことができるかどうかについての指導と学習評価について悩んでいます。図形の証明における学習評価を進めるときのポイントはありますか。

Ａ　次のポイントを意識してみましょう。

　前回は、証明を書くことができるようにするための指導として、授業においては証明の方針や構想を話し合うなどして、証明に取り組むことについてお伝えしました。今回は「証明を書くこと」について、学習評価の側面で考えてみましょう。

　「指導と評価の一体化」のための学習評価に関する参考資料（国立教育政策研究所）において、第２学年２B（２）「図形の合同」には下のような評価規準例が示されています。

　生徒が図形の性質を証明することができるかどうかの評価について、この評価規準例に対応させて考えてみます。

□三角形の合同条件などを基にして三角形や平行四辺形の基本的な性質を論理的に確かめたり･･･

　

　前回、論理的に考察する力について、数学的推論（帰納、演繹、類推）を例にお伝えしました。 中学校数学では問題解決の際に演繹的に推論することを重視しており、図形の性質を証明することはその1つの活動です。授業では、証明を書くことに偏り、つい書き方の指導になってしまうことがあります。書き方を指導するというよりも、「何か明らかにしたいことがあるとき、それが成り立つことを筋道を立てて説明すること」を重視したいですね。さらに、生徒によって書かれた証明に対して、教師によるフィードバックが必要になります。学校においてはテストなどの場面をさします。これに加えて、全国学力・学習状況調査もあげられます。全国学力・学習状況調査を例に、図形の証明における生徒へのフィードバックについて考えます。
　全国学力・学習状況調査では図形の証明について様々な問題が出題されています。その中で「三角形の合同条件などを基にして〜」という視点での問題として、少し前のものになりますが、下のような平成29年実施の数学B大問4(1)と取り上げます。

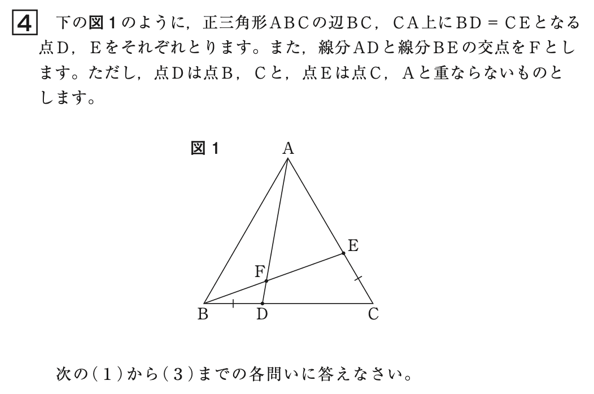
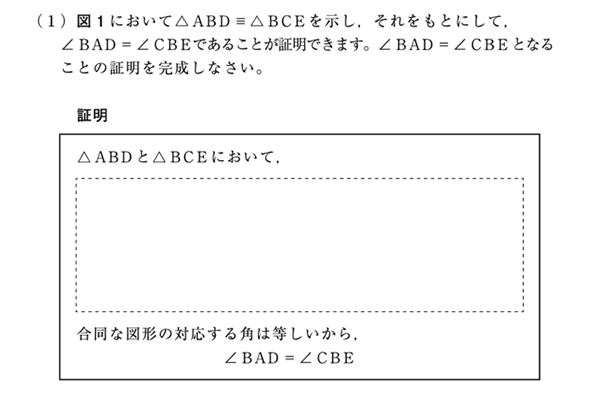
平成29年度全国学力・学習状況調査中学校数学B4(1)

　この問題では、「\(\triangle \text{ABD}\) と\(\triangle \text{BCE}\) が合同になる」という関係を基に「\(\angle \text{BAD}=\angle \text{CBE}\)」になることを証明をすることができるかどうか評価する記述式問題です。評価の観点は現行の学習指導要領においては思考・判断・表現になります。平成29年全国学力・学習状況調査報告書中学校数学によると、正答率は45.0％と報告され、課題があるとされています。この問題について、採点により評価する際には、証明を書くことができた・できないという二択のみで判断するのではないと思います。正答の条件を設定し、それを満たしているかどうかを確認しなければなりません。この問題における証明では、正答の条件として、次の4点を設定することができます。

①\(\text{BD}=\text{CE}\)　②\(\text{AB}=\text{BC}\)　③\(\angle \text{ABD}=\angle \text{BCE}\)　④\(\triangle \text{ABD}\equiv \triangle \text{BCE}\)

　④を示すために必要となる条件としての①、②、③ではありますが、①〜④の条件はこの証明を構成する必要な数学的な事実であり、根拠となるものです。まずはこれらのことが記載されているかどうかを確認します。その上で、①〜④の条件について、それぞれの根拠を記述しなくてはなりません。この根拠とそれによっていえる事実の記述を全国学力・学習状況調査では理由の説明として評価をしています。
　テストなどの評価場面だけでなく、生徒の記述や口頭での発表、さらにはグループによる証明活動などにおいて生徒の理解の状況を把握する際に、証明を構成する必要な条件とその根拠が表現されているかどうか、指導者が明確することが大切です。そして、理由の説明として十分であるのか不十分であるのかについてしっかり把握し、促していくことが求められます。

　証明を書くことができるようにするために、評価する際の視点（正答の条件）を数学的な推論の考え方と合わせて明確にします。その上で、書かれた証明について、単純に正誤をつけるのでなく、証明を構成する条件について根拠を示して説明しているかどうかを確認し、それをフィードバックすることが大切です。

　次回は、「証明を読んで新たな性質を見いだしたりすることができる」について取り上げます。

※参考資料

• 「指導と評価の一体化」のための学習評価に関する参考資料
• 平成29年全国学力・学習状況調査報告書中学校数学

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。