特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

教材研究と授業づくりの進め方〜課題や問題設定の工夫〜

Q　授業での課題や問題設定について、大切なポイントはありますか？

Ａ　次の3つのポイントを意識してみましょう。

1. ① 学びのゴール（資質・能力の獲得）と、それにつながる既知について明らかにする
2. ② 問題解決のために生徒の既知と未知の状況を明らかにする
3. ③ 生徒が問い続けることができるよう場面を工夫する

　課題や問題設定は、その時間の問題解決において生徒自らが問いを持つことになる大切な場面といえます。主体的に学びを進めるために、教師は生徒が問いを持つことができるよう工夫をしたいですね。

　このことを、第2学年2章「連立方程式」における「連立方程式の解き方」について考えてみましょう。数学の学習では様々な“計算”があります。“計算をできるようにする”技能を中心として指導される方もいらっしゃると思いますが、「計算方法をしっかり教え、繰り返し練習させる」だけの指導になってはいないでしょうか。

　中学校学習指導要領（平成29年告示）数学解説編では次のような記述があります。

文字を用いた式、方程式を解くことなどの技能を学ぶ際には、その手続きの基礎に概念や原理・原則があることや概念や原理・原則をうまく使って数学的な処理の仕方が考え出されることを理解することが大切である。

（中学校学習指導要領（平成29年告示）数学解説編p.25より引用）

　計算方法について概念や原理・原則を用いて、生徒が生み出していく授業を求めていることがわかります。学んだ数学を基にして、未知の計算方法について「同じように考えてもよいことはないか」「新たに考えるべきことは何か」などを検討しながら、計算の可能性や手順を見いだし、生徒が計算の方法を考えるのです。その際、数学的な見方･考え方を働かせることができるよう授業の様々な場面の工夫が大切であり、その一つとして問題設定や課題の設定があります。

　このことについて、「新しい数学2」2章「連立方程式」における「連立方程式の解き方」の第1時（p.40,41）を例に考えてみましょう。

①　本時の学びのゴール（資質・能力の獲得）とそれにつながる既知について明らかにする

　授業づくりを進めていく際に、本時の学習内容だけでなく、本時に関連する内容について事前に確認することがあります。いわゆるレディネスです。例えば、直近の学習内容である「二元一次方程式とその解の意味」「連立方程式とその解、または解くことの意味」などがありますが、授業での生徒の問いにつながる課題や問題設定を考えるためには、教師は本時の学習内容と関連が深いものについて教師が予め確認しておく必要があります。

　教科書をみると、p.40の上部には「連立方程式を解くにはどうしたらよいか考えてみよう」とあります。本時が連立方程式を解く方法の説明ができるかどうかを評価しようとしている時間であることがわかりますね。

　教科書p.40の下部には、次のような記載があります。

　これが本時で期待される連立方程式を解くための方法であり、このことを生徒自らが発見できるようにすることが大切です。そのためには、これまでの学習内容の中で何をどのように関連付けて問題解決できそうかを明らかすることが求められます。

②　本時の問題解決のために生徒の既知と未知の状況を明らかにする

　教科書の問題から、生徒が下のような連立方程式をつくり、それを解くという流れを想定してみましょう。既知の方程式との比較を問うことで、生徒は下のような指摘をすることが考えられます。

　さらに、1年生で学んだ方程式について確認すると、「文字が一つで、式も一つであった」と振り返ることでしょう。その上で、「この連立方程式を解くことはできそうか？」「どのようにすれば解くことができるのか？」と問いかけることで、「文字を一つになれば…」かつ「式が一つにできれば…」といった連立方程式の解き方における見通しや構想について立てることにつながり、生徒に自分事の問いが生まれるのです。

　「文字が一つで、式が一つ」という見通しのもと、生徒に想起してほしいことは「一次方程式をどのようにして解いてきたか」です。生徒は、方程式を解くことを単に計算することと捉えているかもしれません。しかし、実は目的に応じて式を変形しているといえます。目的とは何でしょうか。方程式の解を求めるために、「\(Ax=B\)」の形を目的として等式の性質を用いて式変形します。つまり、「\(Ax=B\)」の形に変形できれば方程式の解が見つかると捉え、この形に帰着させて考える「数学的な見方・考え方」を働かせていることになります。これらのことについて教科書を活用して、生徒が見いだすことができる授業としたいですね。

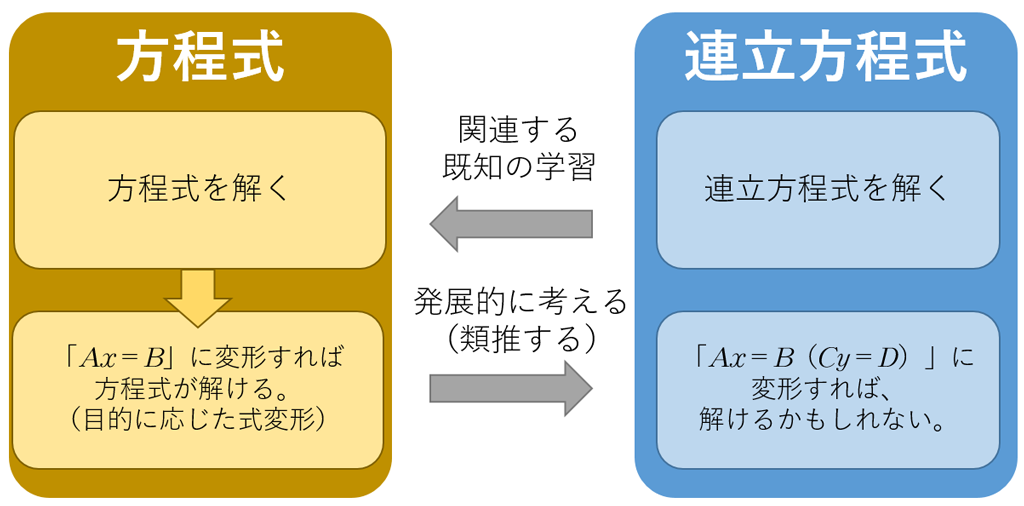
③　生徒が問い続けることができるよう場面を工夫する

　「\(Ax=B \mathrm{(}Cy=D\mathrm{)}\)」を変形の目的とすることで、文字を1つだけ含む方程式をつくることを具体的な問題で確認していきます。この場面も、教師が一方的に説明するのではなく、生徒の問いを大切にして展開するとよいでしょう。教科書p.41には下のように掲載されています。

　教科書p.40では図で考えましたが、今回は「実際に解いてみる」または教科書を読んで「どのようにして解をみつけているかを確認し合う」などの活動が考えられます。ただ取り組ませるのではなく、「連立方程式では、式を変形して文字を1つだけふくむ方程式をつくれば、1年生で学んだ方程式となり、解くことができること」について具体的に確認し、「\(Ax=B \mathrm{(}Cy=D\mathrm{)}\)」を目指して式を変形していることを生徒が指摘することが大切です。
　さらに、生徒が例1を取り組む際には教師はどのような問いかけをすればよいでしょうか。

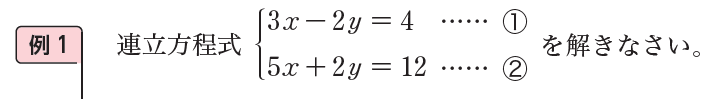
　同じように、「この連立方程式を解くことはできそうか？」「どのようにすれば解くことができるのか？」などと問いかけることで、先ほど取り上げた連立方程式との違いや方程式の \(x\) や \(y\) の係数などに着目をして、「さっきとは違って式どうしをたせばよい」「\(Ax=B \mathrm{(}Cy=D\mathrm{)}\) に変形する」「文字を1つ消去すればよい」などと考え、生徒自らが課題をもって問題解決に臨むのではないしょうか。

　授業では、「めあて」「学習課題」をただ板書すればよいということでなく、その授業で育成を目指す資質・能力を明確にし、その獲得につながる既知の数学について、教材研究を通して明らかにすることが大切です。そして、教師はそれを発問などで働きかけることで、生徒は自分事の問いを持ち問題解決に力強く向かうのです。こうした問いの一つ一つが生徒にとっての“課題”や“問題”になると考えます。

　数学は、統合的・発展的に考えることで新たな数学、次の数学を生み出し深めていくものです。未知を切り拓くために、既知とのつながりを重視することで、たとえ今回扱ったような“計算する”学習場面であったとしても、生徒にとって“深い学び”となるのではないでしょうか。

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。