特集記事（小中学校）

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第6弾になります。

　令和4年度実施の全国学力・学習状況調査 中学校数学大問3を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：作図などの活動を通して、反例の意味を理解すること

※全国学力・学習状況調査より

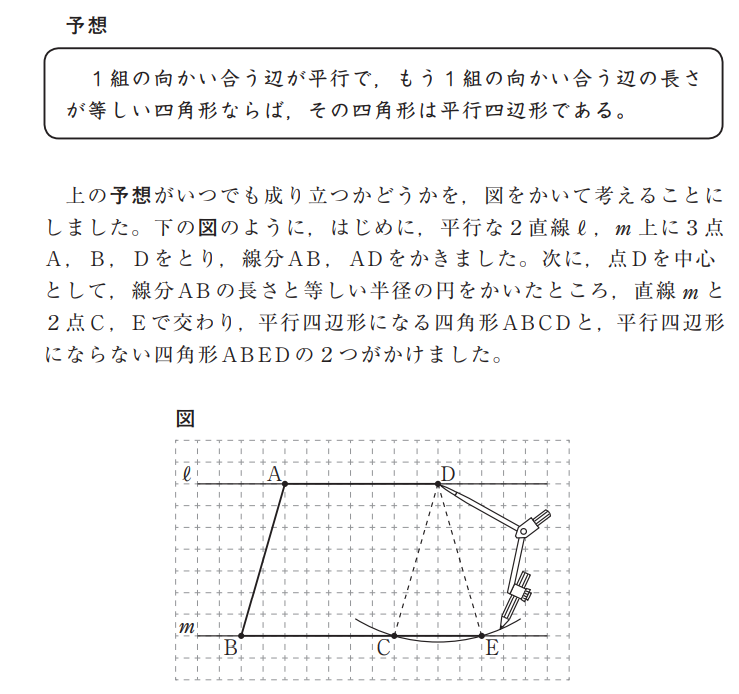
　大問3は、反例の意味を理解しているかどうかをみる問題です。第2学年では、命題が常に成り立つことや常に成り立つとは限らないことを示すことについて学習します。命題が常に成り立つ場合には証明をすること、それに対して、命題が常に成り立つとは限らないことを示すには反例を1つあげることで説明します。

本問は、予想した事柄「1組の向かい合う辺が平行で、もう1組の向かい合う辺の長さが等しい四角形ならば、その四角形は平行四辺形である。」について、成り立つか成り立たないかを考えます。

示された図をもとに考察する際に、「1組の向かい合う辺が平行で、もう1組の向かい合う辺の長さが等しい四角形」という仮定条件で作図された四角形が、平行四辺形ABCDと（等脚）台形ABEDの2つであることを確認し、平行四辺形にはならない四角形を見いだすことで予想した事柄が成り立たないことを説明することが大切です。示された図から（等脚）台形ABCDを見いだすことができるかどうかで、選択肢「ア、イ」と、「ウ、エ」の選択につながります。

選択肢「ア、イ」のうち、「イ」を選択する生徒は、数学的な推論として帰納的に考えることと、演繹的に考えることについての理解に課題があると考えられます。予想した事柄が成り立たないとした選択肢「ウ、エ」について、「エ」を選択する生徒は、推論の際にいくつかの例で成り立つかどうかを考えるといった帰納的な推論と混同していることが考えられます。命題が常に成り立つとは限らないことを示すには、反例となる図を作図して確かめることができることを解決の際の活動として取り入れることや、反例を1つあげることで説明できるかどうかについて話し合う場面を取り入れることが大切です。

POINT②：見いだした図形の性質や関係を論理的に確かめる場面を設定すること

　本問は、評価の観点として「知識・技能」となっています。授業では、命題や推測した事柄についての成り立つかどうかについて考察する際に、論理的に説明するといった数学的活動を充実させるとともに、数学的に説明することを「思考・判断・表現」として評価することも考えられます。

例えば、平行四辺形になるための条件「1組の対辺が平行でその長さが等しい」を見いだした後に、「1組の向かい合う辺が平行で、もう1組の向かい合う辺の長さが等しい四角形ならば、その四角形は平行四辺形であるといってよいか」などと問い、成り立つかどうか論理的に説明する場面を設定するとよいでしょう。その際に、仮定である「1組の向かい合う辺が平行で、もう1組の向かい合う辺の長さが等しい四角形」という条件をもとに作図し、結論について考えます。

本問では「図」のように（等脚）台形ABEDがかけることから、これを反例とし、平行四辺形になるという結論が成り立たないことを判断し、それを発表したりノートに書いたりして説明することができるようにすることが大切です。その際に、反例が仮定を満たしているが結論を満たしていない例であることを併せて確認することも考えられます。

POINT③：教科書の構成を生かして授業を構想すること

　教科書では、ある定理の仮定と結論を入れ替えたものとしての定理の逆について取り上げるとともに、その定理の逆が成り立たないことについて説明する場面を設定し、反例の必要性と意味について考える場面が設定されています。具体的な場面を紹介します。

　教科書p.135の問2において、命題や推測した事柄について、その逆を表現することを問題として取り上げています。その中の(2)「2つの三角形が合同ならば、その2つの三角形は面積が等しい。」を取り上げ、その逆を「2つの三角形の面積が等しければ、その2つの三角形は合同である。」と表現し、これが成り立つか成り立たないかについて考察する場面を設定します。

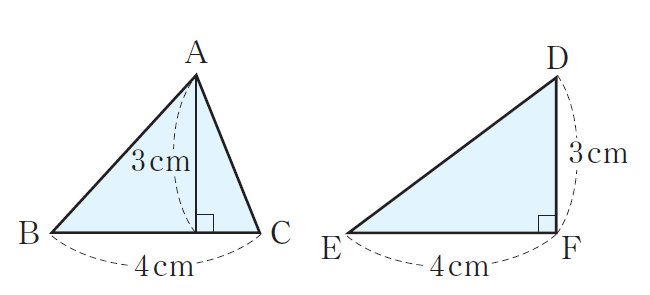
教科書では、三角形を具体的に考え、図を掲載し、下のような底辺が4cmで高さが3cmである\(\triangle\)ABCを示しています。この\(\triangle\)ABC以外に面積が12cm\(^{2}\)となるよう仮定を満たす三角形を実際かくことができるかどうかを検討することを促し、面積が12cm\(^{2}\)となるよう仮定を満たす三角形を取り上げ、それらに合同の関係がないことを確認することが大切です。

このことを通して、\(\triangle\)ABCと\(\triangle\)DEFは等積三角形の関係であるが、合同の関係にはならないことに気付き、これを反例として、「2つの三角形の面積が等しければ、その2つの三角形は合同である。」が常に成り立つとは限らないことを説明するのです。

　

　さらに教科書p.135の問2(3)では、「 \(x \geqq 5\) ならば \(x \gt 3\) である」ことの仮定と結論を入れ替え、「 \(x \gt 3\) ならば \(x \geqq 5\) 」が正しいかどうかを検討することが取り上げられています。数直線を用いて確認することで正しくないと気づき、それを説明するために反例となる \(x=4\) を用いて、結論である \(x \geqq 5\) が満たしていないことを説明することが大切です。

命題や推測した事柄が常に成り立たないことを、反例をもって示すことが、「図形」の領域だけでなく、「数と式」の領域においても使うことができることを知り、領域に限らず反例を用いて考察することのよさを確認する場面を設けるとよいでしょう。