特集記事（小中学校）

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第5弾になります。

　令和4年度実施の全国学力・学習状況調査中学校数学大問8を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：一次関数や比例とみなして問題解決すること

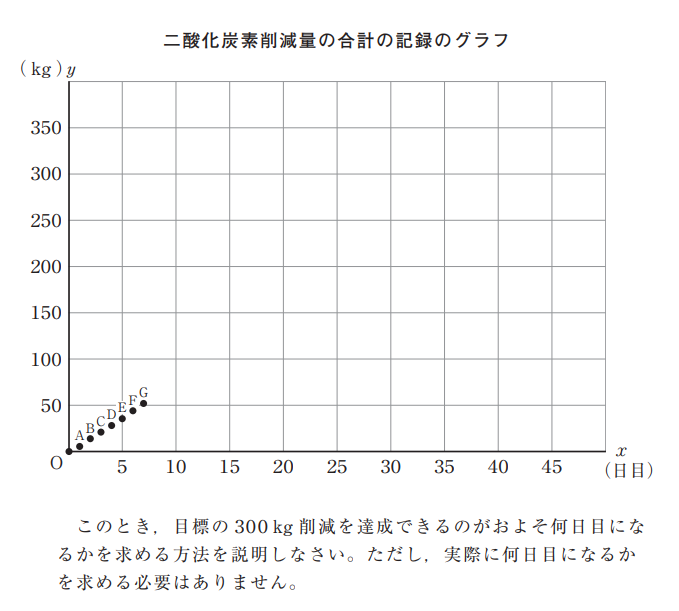
※全国学力・学習状況調査より

　大問8は2つの問題で構成されています。(1)は、与えられた表やグラフから、必要な情報を適切に読み 取ることができるかどうかを評価する問題です。二酸化炭素削減の取り組みを行い、そこで得られたデータ を表にまとめ、グラフに表すことで取り組んだ日数\(x\)と二酸化炭素削減量\(y\)の関数関係を捉え、問題解決 に向かうという場面です。(2)は、事象を数学的に解釈し、問題解決の方法を数学的に説明することができるかどうかをみる問題です。二酸化炭素削減量について、立てた目標300kgがいつ達成できるのかを、表・ 式・グラフを利用して明らかにします。特に(2)は、授業において生徒どうしで話し合ったり、発表した りと数学的に説明することが大切です。指導の際に大切なこととして、以下2つを取り上げます。

①取り出した2つの数量について、事象を理想化したり単純化したりして一次関数や比例とみなすこと

　データをプロットした点について、すべて一直線上にあるといえませんが、一方で、ほぼ一直線上にあるとみることもできます。そこで、点がすべて一直線上にあるとし、二酸化炭素削減量\(y\)が日数\(x\)に比例するとみなすというように、具体の関数関係を仮定することができることについて確認します。このことがなかなか受け入れられないという生徒もおりますので、授業では、厳密にはそうはいえないが問題解決するためにある関数関係を仮定することができることについて、丁寧にやりとりをするとよいです。

②捉えた関数関係の特徴をもとに、表・式・グラフを用いて考察すること

　二酸化炭素削減量\(y\)が日数\(x\)に比例するとみなしたことで、比例の特徴を確認し、目標である二酸化炭素削減量が300kgを「\(y=300\)」として、これに対応する\(x\)の値を調べるといった数学的な問題を焦点化して授業を進めることが大切です。実際には、原点を通る直線のグラフを実際にかき、\(y=300\)のときの\(x\)の値をグラフから読み取るといった活動となるでしょう。その際に、表・式・グラフそれぞれの調べ方について比較・検討する場面を設けることも大切です。

POINT②：問題解決の方法について説明する場面を設定すること

　全国学力・学習状況調査中学校数学では、関数の領域における記述式の問題として「方法の説明」が何度も出題されていますが、その正答率は低く、問題解決の方法について数学的に説明すること課題があると指摘されてきました。過去の結果を踏まえると、「グラフをかくとわかる」、「式をつくればわかる」などの、表・式・グラフをどのように用いたのかについての説明が不足することが本問においても予想されます。授業では、説明の正しい書き方に終始するのではなく、授業導入時での問題解決をするための見通しの場面と問題解決後の振り返りの場面を設定し、生徒が自身で数学的な表現の変容を確認したり、全体でまとめたりすることが考えられます。

例えば、「原点0を通る直線のグラフかき、\(y=300\)のときの\(x\)座標を読む」のような問題解決の方法をノートなどに書き、それを共有した後に、導入で立てた方法の見通し「グラフをかくとわかる」と比較し、問題解決のための方法として、グラフのどのようなところに着目し、また、どのように考えたかといった、生徒が働かせた数学的な見方・考え方について振り返ることが大切です。

POINT③：教科書の構成を生かして授業を構想すること

　教科書には、取り出した2つの数量を理想化したり単純化したりして、事象をある関数とみなして考える問題解決の場面が設定されています。教科書を用いて、実際に理想化したり単純化したりして問題解決することを体験的・経験的に学習することが大切です。具体的な場面を紹介します。

　教科書p.145〜146では、「深い学び」として、ある2つの数量の関係比例とみなして問題解決する場面が設定されています。具体的には、ポップコーンを買うためにできた長い行列の最後尾に立つはるかさんが、ポップコーンを買うまでの待ち時間を予想するものです。

　イラストでは、はるかさんが並び始めたときに20番目に位置していることがわかりますが、5分後には12番目となっていたことから、待ち時間を予想する方法を考えます。授業では、5分で8人が買い終えたことを読み取り、1人が買うのにかかる時間に着目をして考察を進めます。その際に、1人が買うのにかかる時間が同じであると考えるかどうかについて、学級で話し合う場面を設定することが大切です。

行列が一定のペースで進むとすれば、1人が買うのにかかる時間が同じになるとみることができることについて共有し、並んでいる人数と待ち時間との関係を比例とみなすことで問題解決を進めていくことが大切です。1人が買うのにかかる時間は、厳密には異なるでしょう。しかし、この場合には、販売されているのがポップコーンのみであることや、イラストの行列をみると人が等間隔で並んでいることなどから、1人が買うのにかかる時間が同じになると理想化したり単純化したりして、比例とみなすことができます。このようにして、ある関数関係を仮定することのよさについても振り返ります。

なお、授業の最後に問題解決の過程を振り返る際には、教科書p.248〜249にある「比例とみなして予想する」というところについて授業で取り上げることも考えられます。授業での生徒が遂行した問題解決の過程と比較をしながら、取り出した二つの数量の関係を比例とみなして、その関係を利用して問題を解決することができる場合があることを確認することが大切です。