特集記事（小中学校）

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第4弾になります。

　令和4年度実施の全国学力・学習状況調査 中学校数学大問4を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：一次関数の変化の割合の意味を理解すること

※全国学力・学習状況調査より

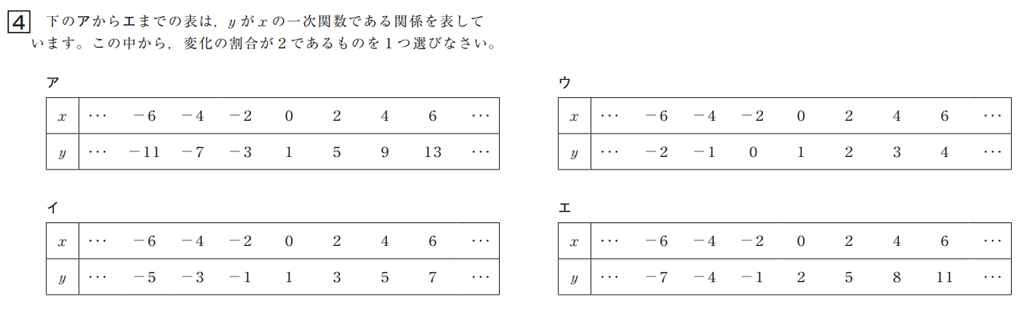
　この問題は、一次関数の変化の割合の意味を理解しているかどうかをみる問題で、知識・技能を評価するものです。生徒はこれまで、関数関係にある二量を取り出し、表、式、グラフを用いてそれらの変化や対応に関する特徴を考察し表現することについて学習してきました。第2学年ではこれらの学習を生かして、一次関数の特徴について表、式、グラフで捉え、一次関数の理解を深めます。

本問においては、一次関数の変化の仕方を捉えるのに必要な\(x\)の増加量に対する\(y\)の増加量の割合である変化の割合について、表から読み取ることができるかどうかを問うものとなっています。4つの選択肢における表をみると、\(x\)は常に2ずつ増えています。表の\(x\)は1ずつ増加していると誤解とすると、一次関数\(y=ax+b\)において、一定の値aは\(x\)の増加量が1のときの\(y\)の増加量であることと混同し、選択肢ウのような\(x\)が0の隣の値に対応する\(y\)の値を増加量とし、それが2であることからこれを選択することが考えられます。もしくは、\(x\)が1ずつ増加しているとし、\(y\)の増加量が2であるイを選択することも考えられます。表における\(x\)が常に1ずつ、常に2ずつ、常に3ずつなど増加していたとしても、変化の割合は\(x\)が1だけ増加したのときの対応する\(y\)がどれだけ増加するかを表しているかを示すものであることを、単に計算するだけにとどまらず、確認することが大切です。

POINT②：後の学習へのつながりを意識して指導する

　関数の考えをもとに問題解決する場面においては、関数関係にある二量における変化や対応を調べることは、小学校算数第4学年より学習が始まります。「新しい算数4下（東京書籍）」をご覧いただけるとよいです。特に中学校の先生に見ていただきたいです。それを見ますと、児童が与えられた表を変化や対応にどのように着目し、問題解決のために生かしているか、ということがわかるでしょう。こうした数学的な見方・考え方を中学校でも引き継ぎ、指導することが大切です。

　また、中学校第3学年「\(x\)の2乗に比例する関数」では、その特徴として変化の割合に着目し、それが一定ではないことを、一次関数と比較をしながら確認するとよいでしょう。\(x\)の増加量に対する\(y\)の増加量の割合である変化の割合を理解することは、高校数学での平均変化率、微分法などの学習にもつながりことを考え、その計算だけでなく、表を使って変化の割合を調べ問題解決をすることを通して、その意味を理解することができるよう授業づくりに取り組むとよいです。

POINT③：教科書の構成を生かして授業を構想する

　教科書を読み解くことで、授業の充実につながるヒントがみつかるものです。本問を受けて、\(x\)が常に2ずつ増加するといった表を与え、変化の割合について考えるといった場面づくりも大切かもしれませんが、教科書を用いて、生徒が変化の割合を用いて問題解決することを通して、その意味を確認することも大切です。具体的な場面を紹介します。

　変化の割合についての学習は、p.63〜64が主な場面となりますが、実際に変化の割合を調べ、それを利用して問題解決するといった学習場面を生かし、変化の割合についての理解を深めることが大切です。

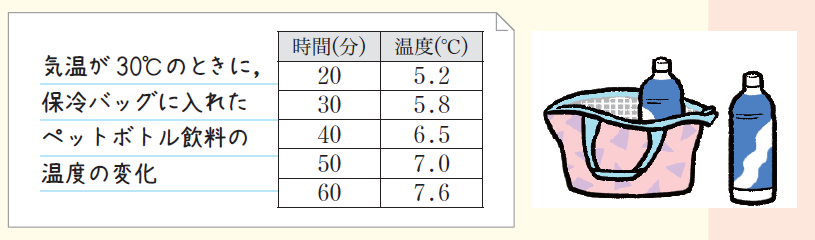
　教科書p.83〜84では、「深い学び」として、一次関数を利用して問題解決する場面を設定しています。具体的には、保冷バックに入れたペットボトル飲料がいつまで冷たいかどうかを考えるものです。気温が30℃のときに、保冷バックにいれたペットボトル飲料の温度変化について実験し、そのデータをもとに考えます。

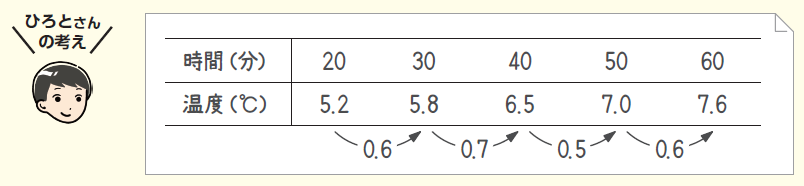
　授業では、ペットボトル飲料の温度が、時間の関数であることを確認した後、取り上げた二量にどんな関数関係があるかについて考察します。その際に、既習である、比例、反比例、一次関数のどの関係になっているかを確認する際に、表における二量の変化に着目して考え、\(x\)の増加量、\(y\)の増加量を調べることを通して、時間が0分のときに温度が0℃にはならないことや時間を2倍、3倍しても、温度が2倍、3倍、もしくは\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍にならないことを確認し、二量が比例や反比例の関係ではないことを確認します。さらに、変化の割合を調べ、温度はおよそ0.6ずつ増加しているとみることができることを確認します。このとき、時間が10ずつ増加すると、温度は0.6ずつ増加しているとみなして考えるわけですが、教科書に記載がないことを生かして、表において時間が常に10ずつ増加するときの\(y\)の増加量を考えていることを生徒と確認しながら授業を進めることが大切です。