特集記事（小中学校）

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第3弾になります。

　令和4年度実施の全国学力・学習状況調査中学校数学大問2を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：方程式を的確に解くために、方法を理解すること

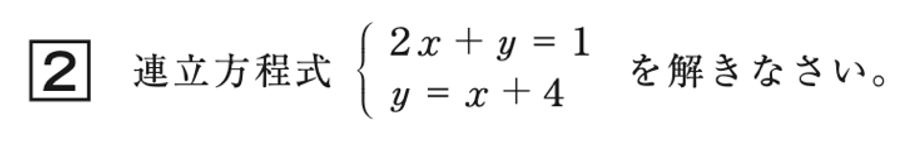
※全国学力・学習状況調査より

　この問題は、簡単な連立二元一次方程式を解くことができるかどうかをみる問題で、知識・技能を評価するものです。連立二元一次方程式を的確に解くことができるようになることは、今後の問題解決にとって必要なことです。連立二元一次方程式を解くことは大切ですが、その解法について生徒どうしで確認しながら進めることも大事したいです。

　例えば、連立二元一次方程式を解く際には、1年生での一元一次方程式の解法について振り返り、「\(Ax=B\)」という形にすればよいことを確認するとともに、文字を消去することが必要であることへの気づきが大切です。連立二元一次方程式を解く際に、「加減法」「代入法」のどちらが優位かではなく、2つのうち一方の文字を消去するために用いている方法であることを確認しながら、どの方法を用いてどのように解いたのかといった過程が大切です。しかし、式によっては「加減法」「代入法」のどちらかが進めやすいということもあります。結果的には、どちらの方法でも構わないが式の形に応じて、よりよい方法を生徒自身が選択し、その選んだ根拠を式の形に着目して説明できるとよいでしょう。

　解法について授業で取り上げる際には、教師が一方的に伝えるのではなく、「加減法」「代入法」のどちらで解いたか、そのことによってどんなよいことがあったのかなど生徒どうしで確認し合うことも考えられます。

POINT②：後の学習へのつながりを意識して指導する

　全国学力・学習状況調査では、単に方程式を解くことができればよいといった数学的な処理のみを考えているわけではないことが国立教育政策研究所から出されている全国学力・学習状況調査の解説資料から伺えます。解説資料p.14の出題の趣旨の下には、次のような記載があります。

「本問は、簡単な連立二元一次方程式を解くことができるかどうかみる問題である。連立二元一次方程式を的確に解くことは、具体的な問題を解決したり、二元一次方程式のグラフについて考察したりする際に必要であるから出題した。」

　本問の式をみると、その形から様々な事象を思い浮かべることができますが、特にも一次関数の単元における、二元一次方程式のグラフ、そして、2直線の交点座標を求める場面が想起されます。このとき連立二元一次方程式を的確に解くことが求められます。教師は、そのことを意識して連立二元一次方程式を解く生徒の様子を把握する必要があります。単元の学習が進むにつれ、方程式の係数に、小数や分数が含まれるようになりますが、このことも後の問題解決場面で扱うことが想定されますので、教師は見通しを持って指導する必要があります。なお、後の学習について、過度に生徒に伝える必要はありません。

POINT③：教科書の構成を生かして授業を構想する

　教科書を読み解くことで、授業の充実につながるヒントがみつかるものです。このことについて2つ紹介します。

　これは、代入法を学習する場面の問題提示です。学習した「加減法」でも解くことはできますが、教科書の記載と、「加減法以外でも解く方法はありますか？」や「加減法以外でも解く方法をみつけましょう」など教師の発問と連動させることで解法をひろげることができます。さらに、2つのうち一方の文字を消去すればよいという方程式を解く際の、式変形の目的は変わらないことへの確認につながる問題提示になっているとかんがえられます。代入法を用いて解くといった例題を与え、その解き方を一方的に解説するのではなく、生徒自らが加減法以外の解法を考える授業を構想することができます。

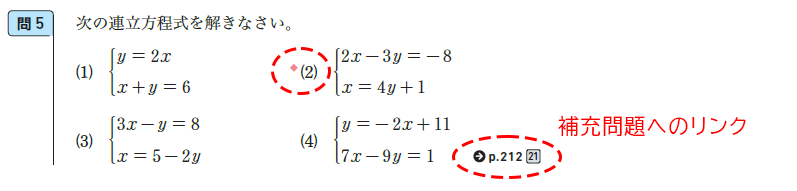
　教科書には、練習問題として多くの問題が掲載されています。これらの問題は、全て取り組まなければならない、みんな一律に取り組まなければならないのではなく、指導する教師は生徒の実態に応じて進め方や問題の量を適切に判断する必要があります。教科書では、問題に「◆」がついているものがありますが、これは構造的に例題に近い問題です。例えば、このような問題については全員で取り組み、優先的に解法をみんなで確認することが考えられます。また、もっと解いてみたいと思う生徒や多くの問題に触れさせたいときには巻末にある補充問題に取り組むことも考えられます。2年生という学年も踏まえると、多くの問題にチャレンジしたい生徒は、自分で該当ページを開き取り組むことができるようになるとよいです。