神奈川県立横浜旭陵高等学校
持丸 裕一 先生
また,誤答や多様な考え方を引き出すことができ,それらを検証する過程で主体的な活動が生まれ,深い理解につながります。
過去3回のレポートでは,例や例題の内容をより深く理解させるために,問題を解いた後で5分間のシンキングタイムを設けました。今回は,例や例題を考える前にも5分間のシンキングタイムを設け,解いた後のシンキングタイムとの相乗効果で,さらに学びを深めます。

三角比の単元の最後にある,空間図形の計量の例題です。
空間図形を苦手に感じる生徒は多く,ましてやその断面図となると,想像できる生徒はかなり少ないのではないでしょうか。通常の授業では,教科書に載っている見やすい図を頼りに問題を解かせ,三角比が図形の計量に有用であることを実感させますが,同時に空間における直線や平面の位置関係もイメージできるようにしてあげたいものです。
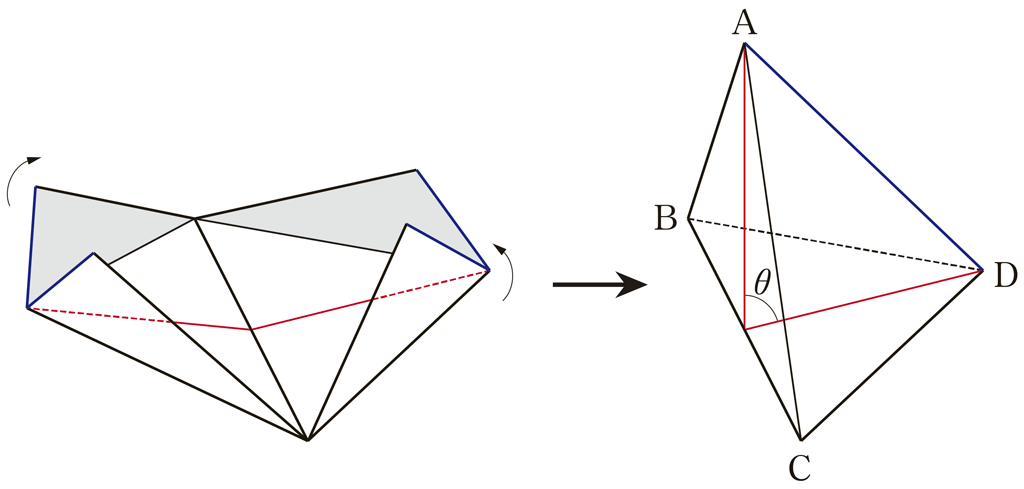
そこで,正四面体を実際に見ながら考察することを考えます。次のようにすれば,古封筒1枚で正四面体を作ることができます。
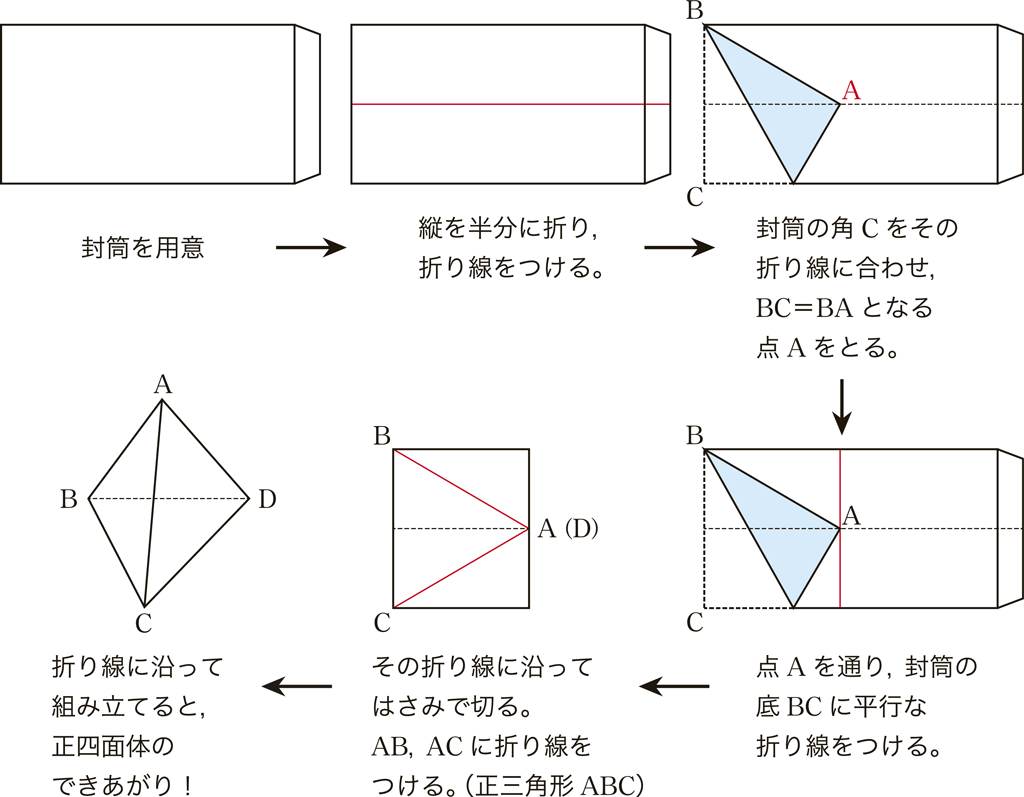
ここで,例題7の \(\theta\) をイメージしやすくするために,短い時間で「予想を取り入れた」次のような発問をします。
作った正四面体を \(\text{A-BCD}\) とします。\(\triangle\text{ABC}\) の面と\(\triangle\text{DBC}\) の面のなす角 \(\theta\) は何度だろうか?予想してみましょう。
T :\(60^{\circ}\) という意見が多いね。では \(60^{\circ}\) 判定機をもってきたから,判定してみなさい。
小さい円に \(60^{\circ}\) の切り込みをいれた紙を全員に配ります。
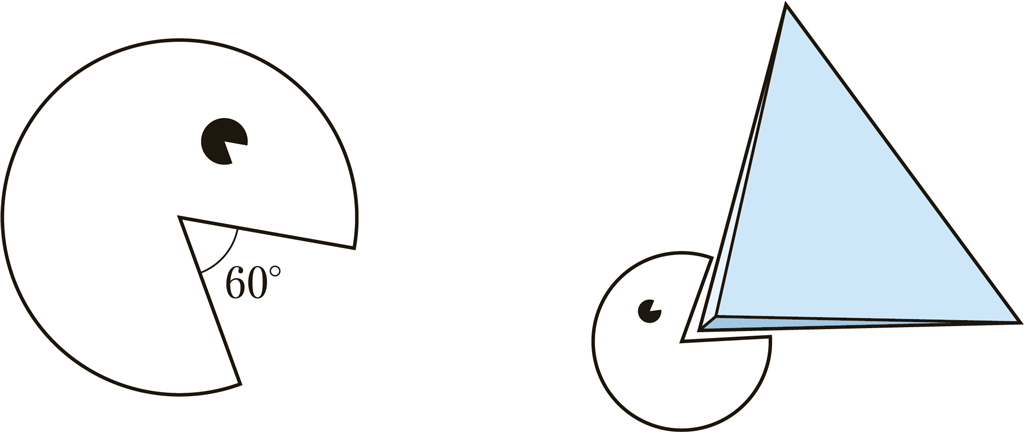
この切り込みを上右図のように正四面体に当てて,予想が正しいかどうか判定させます。
T :予想が外れたみたいだね。それでは,この角度を検討するために,正四面体を半分に切断してみようじゃないか!
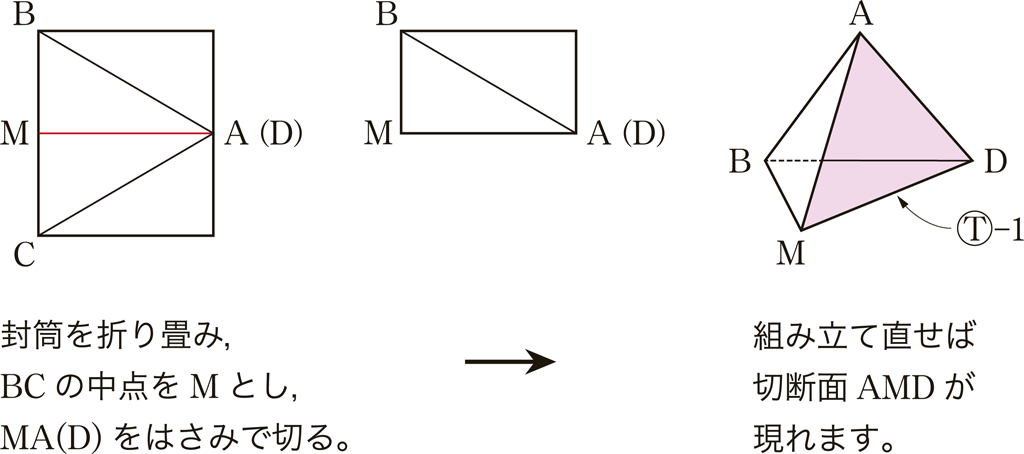
S-3 :切断面を見て,正三角形ではないことははっきりしたけど,何度かなぁ?
T :予想できたら,周りの人に角度を宣言しましょう。
予想した \(60^{\circ}\) と違うことに気づき,理由を知りたくなることでしょう。「なぜ?」「アレ?」という心理は,興味や関心を引き出し,理由を考えようとする動機を与えてくれます。
余弦定理を使って \(\cos\theta\) の値から角度を求めればよいこと,そのためには\(\triangle\text{AMD}\) の3辺の長さが必要であることを確かめます。
S-4 :\((\sqrt{3})^2+(\sqrt{3})^2-2\times\sqrt{3}\times\sqrt{3}\times\cos\theta=2^2\) より,\(\cos\theta=\frac{1}{3}\) だから,三角比の表から \(70^{\circ}\) ~ \(71^{\circ}\) くらいです。
T :すばらしい。予想が当たった人はいるかな?
(2)は,作った正四面体の切断面\(\triangle\text{AMD}\) を見ながら,\(\text{AH}=\text{AM}\sin\theta\) となることを確認すれば,簡単に求めることができるでしょう。断面図を使って考えるよさも実感できると思います。
これで終わらせてしまうのは,もったいないことです。三角比の活用場面を新たに設定し,三角比が図形の計量に有用であることをさらに実感させたいものです。
そこで,例題を終えたあとにもシンキングタイムを設けます。
\(\triangle\text{AMD}\) の面積を求めなさい。
【発問その②】
正四面体の体積を求めなさい。
時間に余裕があるときは,予想の場面を増やすと授業は盛り上がるでしょう。
例えば例題7(1)では,古封筒の活動の前に,次に紹介する活動を追加し,\(\theta\) の求め方についてより理解を深めます。
A4コピー用紙を1枚ずつ配り,四面体を作成します。
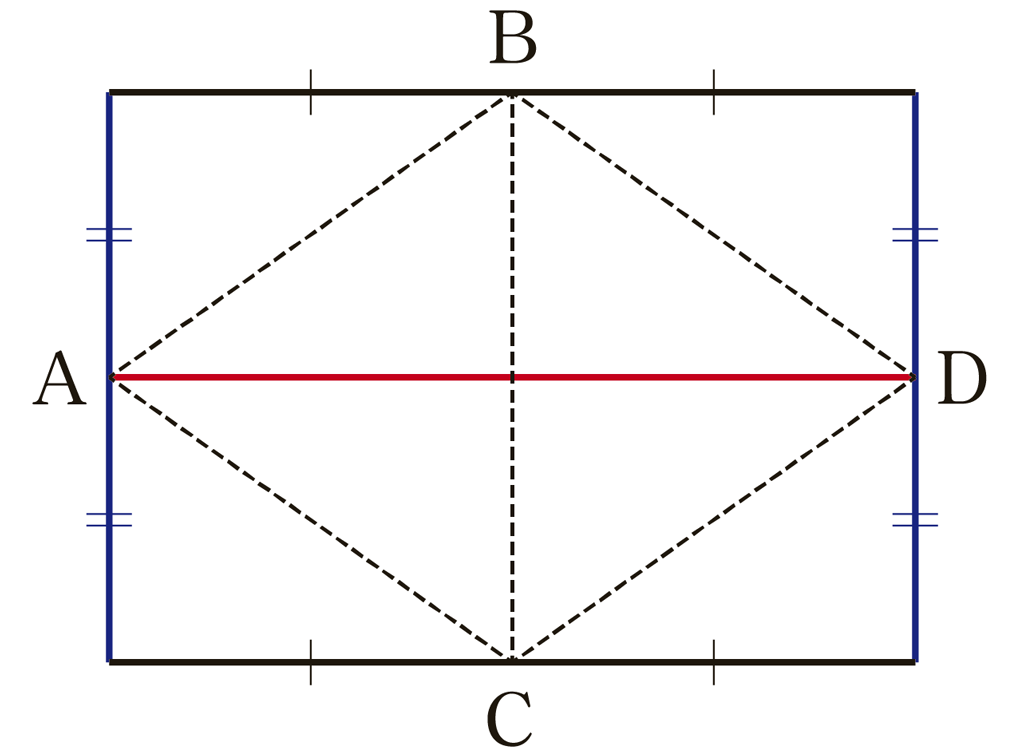
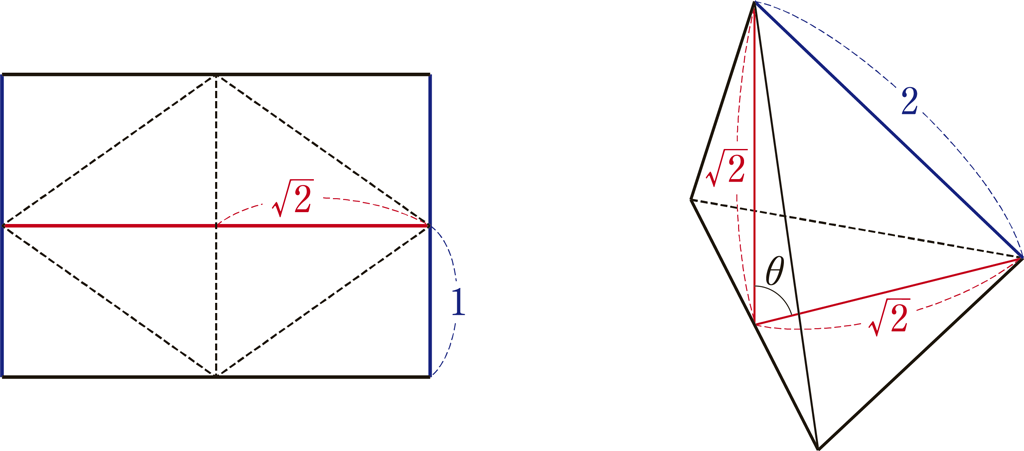
これは,正四面体にはなりません。この模型を使って古封筒の時と同様に,角度に関する【予想を取り入れた発問】をします。青い線や赤い線を引いたのは,断面\(\triangle\text{AMD}\) を意識させるためです。
コピー用紙は,縦と横の長さの比が \(1:\sqrt{2}\) であることから,辺の長さを設定し,先ほどと同じ授業展開から \(\theta=90^{\circ}\) を求めます。
例題7(2)を解いた後には,垂線 \(\text{AH}\) について考察を深めます。そのために,古封筒をもう1枚ずつ配り,新たに正四面体を作らせたあと,予想を取り入れた次のような発問をします。
頂点 \(\text{A}\) から鉛筆を下の面に垂直に立ててみましょう。
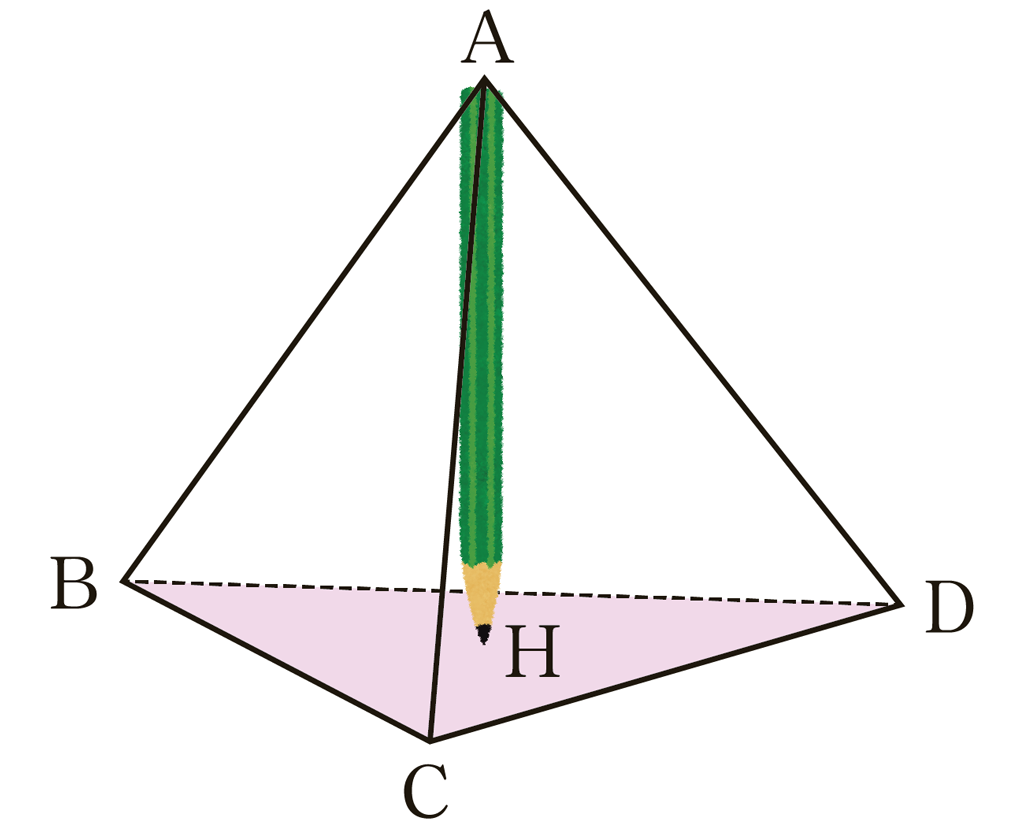
3つの三角形\(\triangle\text{ABH}\),\(\triangle\text{ACH}\),\(\triangle\text{ADH}\) の合同から,点 \(\text{H}\) が外心であることを確認します。余裕があれば,例題7(2)の別解として,正弦定理から \(\text{DH}\) の長さを求め,それを利用して \(\text{AH}\) を求めるシンキングタイムを設けるとよいでしょう。
「予想を取り入れた発問」の中に,「なぜ?」「アレ?」という場面があると,生徒たちは興味関心をもち,理由を考えようとします。考える楽しさを味わうことができ,それが数学のよさを感じ取る原動力となります。
これからも,教科書の問題にひと工夫加えることにより,数学のよさを感じさせ,生徒たちの数学に対する意識を変える授業づくりを目指したいと思います。
その他のコンテンツ
