教科書・教材のひと工夫（高校）

　編集委員の先生方に，2025年を中心に大学入試問題で気になった問題と，あわせて取り組みたい『ニューグローバル数学Ⅲ』の問題を挙げていただきました。
　第1回のテーマは，「一度は経験しておきたい問題」です。

漸化式による三角関数の極限

【編集委員のコメント】

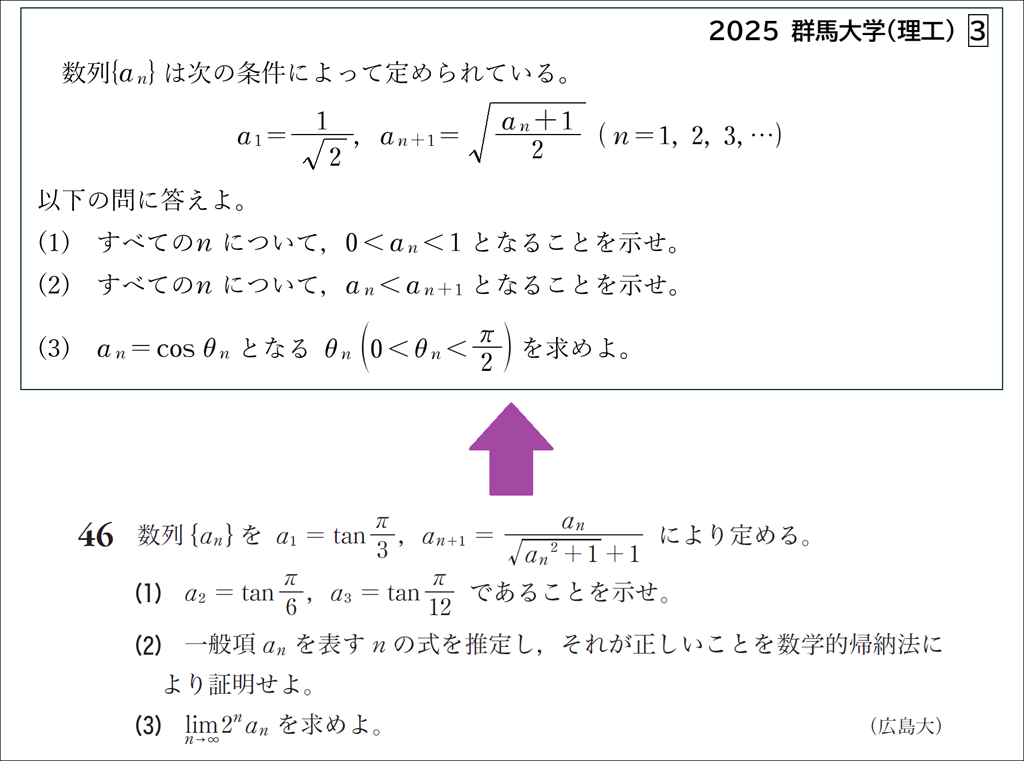
　いずれも，与えられた特殊な漸化式について三角関数を用いて \(a_n\) の正体を掴むタイプの問題で，一度は経験しておきたい内容です。
　グローバル数学Ⅲの問題46は \(\tan \cfrac{\theta}{2} = \cfrac{\tan \theta}{\sqrt{\tan ^2 \theta +1}+1}\) からつくられる漸化式で，\(a_n\) を予想して数学的帰納法で証明する設定になっています。
　群馬大学の問題のように，新たに \(\{ \theta_n\}\) を定義する設定の出題も多いです。例えば1975 年の東京大学では，数列 \(\{a_n\}\) が \(a_1=\sqrt{2}\)，\(a_{n+1}=\sqrt{2+a_n}\) で定義されるとき，\(a_n=2\sin \theta_n\)（\(0\lt \theta_n \lt \frac{\pi}{2}\)）を満たす \( \theta_n\) がどのような式で表されるかを問う問題が出題されました。

媒介変数で表された図形の面積

【編集委員のコメント】

　媒介変数で表された曲線と \(x\) 軸で囲まれた図形の面積に関する問題です。増減表を用いて曲線の概形を描き，状況を掴むことが大切です。
　特に，上の筑波大学の問題とグローバル数学Ⅲの問題162は，\(t\) の範囲内で \(x\) が増加から減少に変化するタイプなので注意が必要になります。決して簡単な問題ではないですが，確実に解けるように練習しておきましょう。

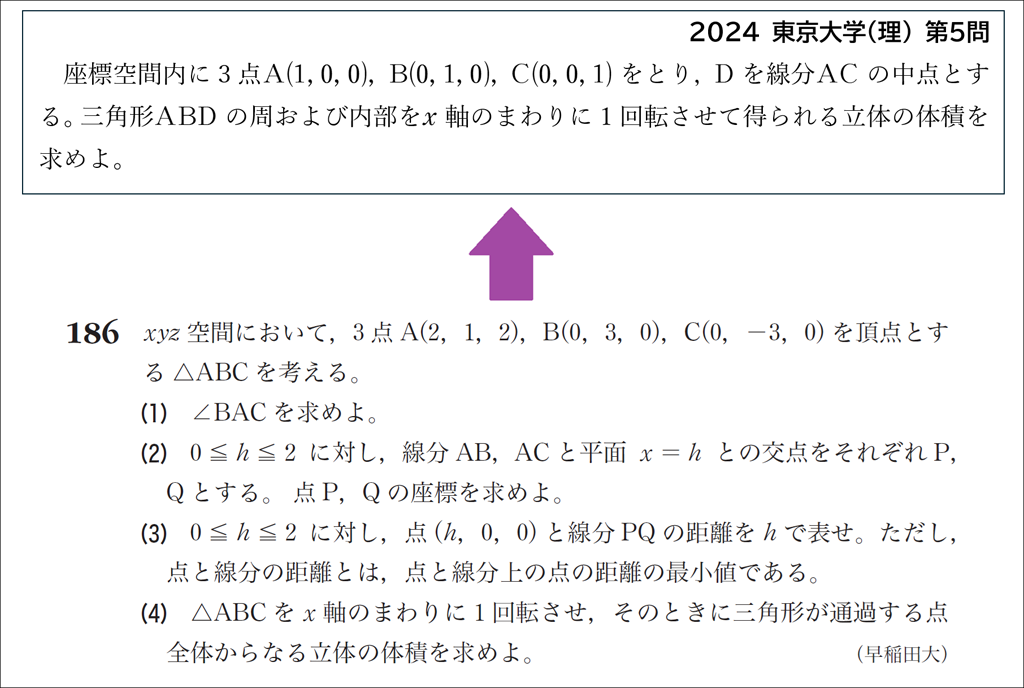
平面図形の回転体の体積

【編集委員のコメント】

　回転体の体積は回転軸に垂直な断面を考えますが，切る位置によって断面の形状が変わる場合は注意が必要です。このタイプも大学入試ではよく出題されます。
　グローバル数学Ⅲの問題186は，適切な誘導がついて考えやすいはずです。東京大学の問題は誘導がないので，問題186をイメージしながらしっかり場合分けができるようにしましょう。是非チャレンジしてもらいたい問題です。
　グローバル数学Ⅲの体積の問題（第17，18項）は良問揃いなので，しっかりと取り組んで力を付けさせたいですね。

アステロイドの道のり

【編集委員のコメント】

　グローバル数学Ⅲの問題191 はアステロイド曲線を題材にした典型問題です。この問題では，点 \(\text{P}\) の座標を媒介変数 \(\theta\) を用いて表せるようにすることと，\(\text{P}\) がえがく曲線の概形を描けるようにすることが大切です。アステロイド曲線については問題166でも扱っています。繰り返すことで定着を図りましょう。
　慶應義塾大学の問題は，内側を回る円の半径が \(r\) のため文字が多くなり混乱しやすいですが，良問なので是非チャレンジしてみてください。特に，(4)の極限はウィットが利いていて面白い内容です。

　いかがでしたでしょうか。第2回は「変化への対応が必要な問題」を取り上げます。お楽しみに！

※入試対策問題集『ニューグローバル数学Ⅲ』の詳細はこちらをご覧ください。