教科書・教材のひと工夫（高校）

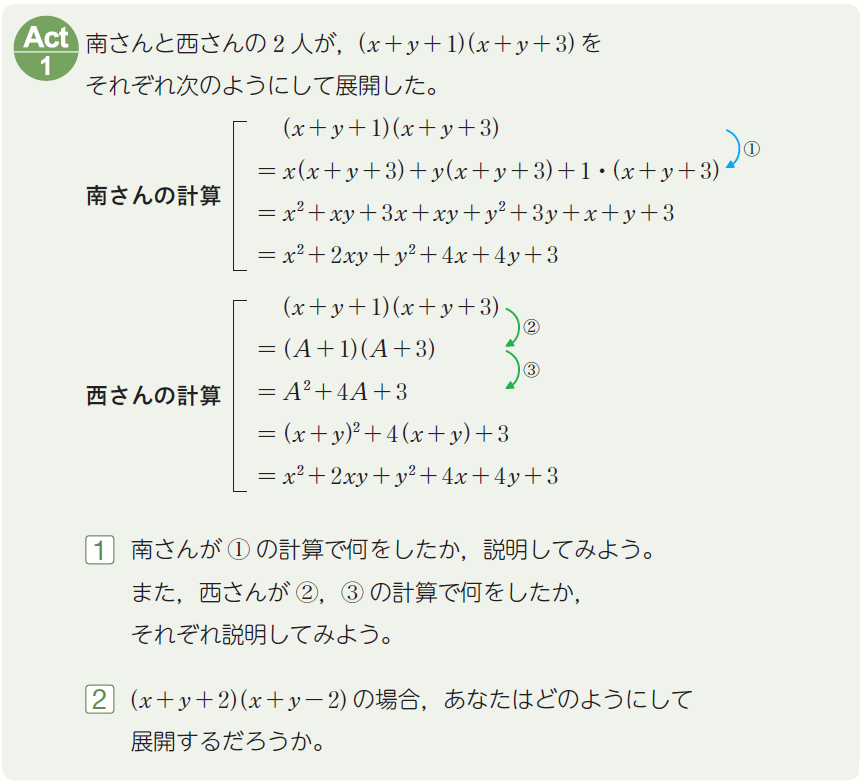
乗法公式の応用（数学Ⅰ）

　置き換えによる式の展開の導入部分で扱うAct.で，\((x+y+1)(x+y+3)\) という式を展開するにあたって，分配法則を利用して1つ1つ展開していく南さんの方法と，\(x+y\) を1つの文字に置き換えて乗法公式を用いて展開する西さんの方法を見せて，それぞれの方法を検討し，比較するという活動を促します。

〈Act.のねらい〉

　この単元の目標は西さんの方法を学習し，使えるようになることですが，南さんの方法と比較することで，そのよさも理解してほしいと考えています。できれば，南さんの方法にも汎用性というよさがあることに気がついてほしいと思います。
　\(\boxed{\ 2\ }\) の「あなたはどのようにして展開するだろうか。」という問いかけに対して，南さんの方法を支持する生徒と，西さんの方法を支持する生徒の両方が出たら，より深い学びを得るチャンスです。双方に支持する理由を説明してもらい，意見を交わしたり，その議論を聞いたりすることで，生徒たちが南さんの方法と西さんの方法のそれぞれのよさを知ることができればと思います。
　一方を支持する意見しか出なかったときは，先生が反対意見に回って，生徒と意見を交わすことも考えられます。

確率の意味（数学Ａ）

　ある試行において事象 \(\text{A}\) の確率が \(\frac{1}{n}\) ということを， \(n\) 回に1回 \(\text{A}\) が起こることだと誤解している生徒は，けっこういるのではないでしょうか。このAct.は，そのような誤解を解き，確率について正しく理解してもらうための問題です。

〈Act.のねらい〉

　東さんの「さいころを3回投げると必ず1回2以下の目が出る。」という考えに対して議論をさせ，正しくないという結論に至れば成功です。
　議論がうまく進まないときは，「では，2回続けて2以下の目が出なかったとき，3回目は必ず2以下の目が出るのか。」と生徒に問いかけてもよいでしょう。もっと単純な例として，「コイン投げで表が出る確率は \(\frac{1}{2}\) だが，コインを投げて裏が出たら次は必ず表が出るのか。」を考えさせてもよいかもしれません。
　これらの議論や発問を通して，事象 \(\text{A}\) の確率が \(\frac{1}{n}\) であるということは \(n\) 回に1回 \(\text{A}\) が起こるという意味ではないということを改めて確認し，確率の意味を生徒に理解してもらいたいと思っています。

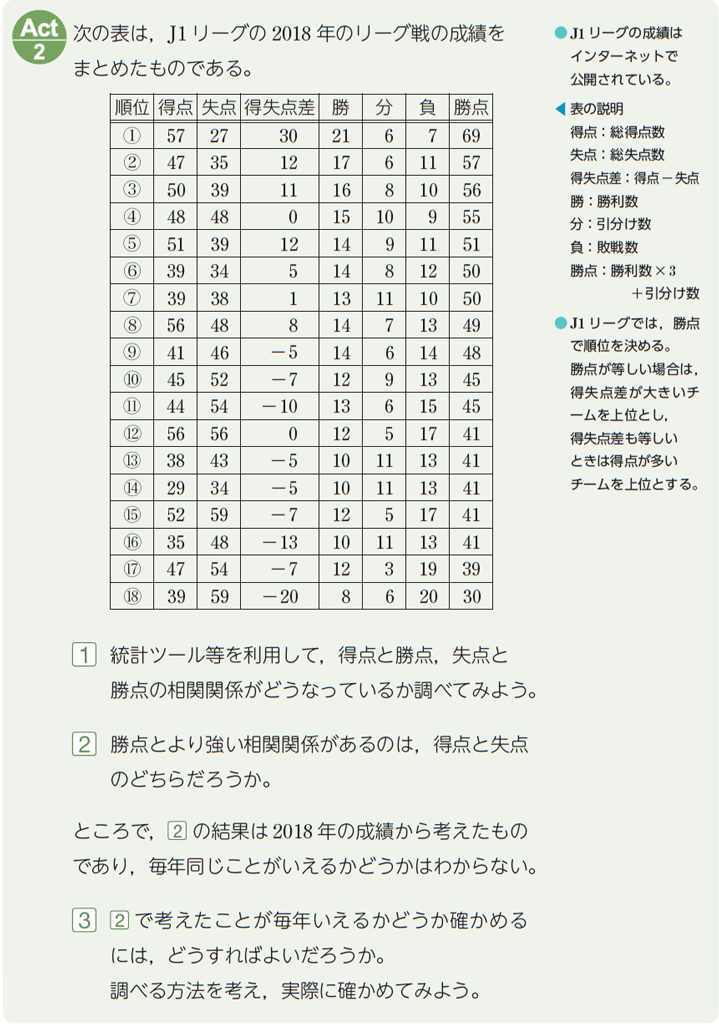
相関関係の利用（数学Ⅰ）

　相関関係について学習した後に扱うAct.で，相関関係を応用することだけでなく，データの分析における問題解決のプロセスであるPPDACサイクルも意識した問題です。

〈Act.のねらい〉

　相関関係は，社会的な問題や自然科学的な問題など様々な問題の解決に利用できる便利なツールです。このAct.では，スポーツの分野で相関関係を利用します。
　球技において，得点をとることに注力する攻撃型のチームと，失点を抑えることに注力する守備型のチームのどちらを志向するかは，チームを運営する上で重要な問題です。この問題を解決するために，\(\boxed{\ 1\ }\)，\(\boxed{\ 2\ }\) ではJ1リーグの2018年の順位表から得点と勝点，失点と勝点の相関関係を調べます。その結果，失点の方が得点より強い相関関係にある，すなわち，守備型のチームの方が強いという結論を得ます。
　ここまではPPDACサイクルの1周目にあたりますが，あらかじめ用意された筋道にしたがって進んでいるので，応用問題と変わりはありません。
　重要なのはその後の \(\boxed{\ 3\ }\) で，いったん得られた結論に対して疑問を呈する一文があります。PPDACサイクルでは，結論を出して終わりではなく，得られた結論に対して検証を行い，不十分であれば，計画を見直したり，異なる方法で分析したり，新たな問題を設定したりして，さらに考察を深めていきます。それを促すのがこの一文で，これを受けて，新たなサイクルを今度は自分で筋道を立てて進めていくことになります。
　\(\boxed{\ 3\ }\) の示唆から他の年の順位表について調べ始めると，失点より得点の方が勝点とより強い相関関係にある年もあることが分かり，守備型のチームの方が強いと一概に言えないことがわかってきます。このAct.に取り組む際は，ぜひ \(\boxed{\ 3\ }\) まで進んでほしいと思います。

　以下，さらに発展的な扱いを紹介します。
　得点，失点で単純に決まらないと分かったとき，何かほかの要素が関係するのかと考えるのは自然な発想です。そこで，順位表の中にある得失点差に着目する生徒がいるかもしれません。そして，この得失点差は，勝点と強い相関関係があります。失う点以上に点を取れば勝てるという，考えてみれば当たり前の結果で，攻守のバランスが取れているチームが強いという結論に至るでしょう。
　このAct.をきっかけにして，スポーツの分野に「データの分析」で学んだことを活用する生徒が出てくれるとうれしいです。

　以上，おすすめの「Act.」のご紹介でした。ぜひ授業でもご活用いただき，生徒のより深い理解や学びにお役立てください。